变分法

[拼音]：bianfenfa

[外文]：calculus of variations

研究泛函的极值的方法。泛函就是函数的函数，给定一个函数集合Y，若对Y中的每一函数y按某一确定的规则J有一确定的实数J[y]与之对应，就说在集合Y上给定了一个泛函J。若泛函J在Y中的y₀处取的值J[y₀]是J在Y中所有的y处所取值J[y]中的最大（小）的一个，则说J [y₀]是最大（小）值，y₀称为最大（小）值函数。设Y┡是Y中在y₀附近的函数组成的子集，若J[y₀]是J在Y┡上取的最大（小）值，则称J[y₀]是极大（小）值，而y₀称为极大（小）值函数。极大（小）值统称极值，极大值函数和极小值函数统称极值函数。变分法的核心问题就是求泛函的极值函数和相应的极值。

变分法的第一个著名例子是最速降曲线问题，它是由约翰第一·伯努利在 1696年以挑战的口吻向当时的数学家提出的。设O和P是铅直平面xOy内高度不同的两点，一质点在重力作用下从O点沿一曲线滑落到P点，假定无摩擦和其他阻力，问曲线呈何形状时其滑落的时间最短？设滑落曲线方程为y=y(x)，由能量守恒定律和弧长公式可知所需时间为

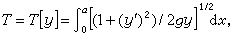　　　 (1)

y的变化范围 Y可取为在区间[0，α]上有一阶连续导数的函数 y的全体。这一问题第二年就由I.牛顿、G.W.莱布尼茨、G.-F.-A.de洛必达、约翰第一·伯努利和雅各布第一·伯努利解决了。

泛函极值的必要条件

和函数极值类似，变分法的第一个基本问题是确定极值的必要条件，这些条件完全以函数的相应必要条件为基础。

固定端点问题

最常见最简单的泛函由积分

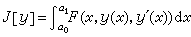(2)

给出，式中F=F(x，y，p)是一个足够光滑的函数，y的变化范围是区间 [α₀，α₁]上所有有一阶连续导数且在两端点分别取定值的函数的集合。设J[y]在y₀取极小值，任取一个在α₀和α₁取零值的函数 η＝η(x)，考虑在函数y＝y₀+tη上J取的值

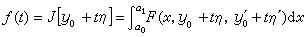， 　(3)

得到一个一元函数，它在t=0取极小值，于是由费马引理得

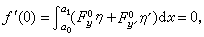　　　(4)

式中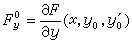等等。(4)式对任意如上的η 均成立，令

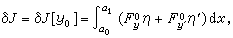　(5)

称它为泛函J[y]在y₀的一阶变分。(4)式无非是说在极小函数y₀处应有

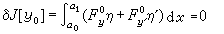(6)

进行分部积分，得

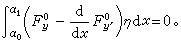　(7)

变分法基本引理　若一个连续函数与足够多的光滑函数的乘积的积分得零，则此连续函数必恒等于零。由此可得极值函数y₀应满足方程

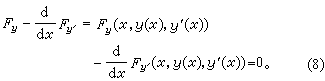
这一方程称为欧拉方程，是L.欧拉在1736年用折线逼近曲线得到的。在1744年的一本书中，他用这一方程解决了大量的泛函的极值问题。这本书标志着变分法作为一个数学分支的诞生。不过这里采用的是 J.-L.拉格朗日于1755年给出的至今仍然普遍采用的变分方法，其基本点是给极值函数y₀以变分η，泛函J[y]相应的变分J[y₀]η应为零。

自由端点问题

把相应最速降线问题泛函(1)的欧拉方程的解用常微分方程的方法解出来得到旋轮线。若参与比较的曲线的端点在直线x=α₀和x=α₁上，但纵坐标未知，在对变分(5)分部积分时将会有附加项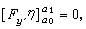η在端点α₀和α₁的值任意，由此知道

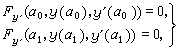　(9)

y自然仍满足欧拉方程。若曲线的右端点在曲线ƒ(x，y)=0上滑动，则在α₁应满足横截条件

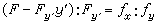。 　　(10)

这类条件是首先由拉格朗日在1760～1761年的一篇文章中得到的。

条件极值问题

若在使与(1)类似的泛函取给定值

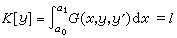　 　　 　(11)

的y中求泛函(1)的极值函数和极值，这就是泛函的条件极值问题。类似于多元函数的拉格朗日乘数法，引入泛函

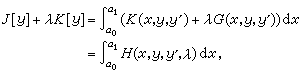　 (12)

则存在常数λ使极值曲线y满足相应于H的欧拉方程，这一方程和条件(11)一般就能确定y。

最引人注目的条件极值问题是等周问题，即在给定周长l 的平面封闭曲线中选取围出最大面积的曲线。对封闭曲线采用参数方程

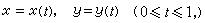
相应周长

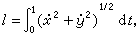
相应面积

。

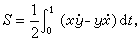
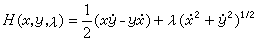对两个函数x和y和(8)相应的欧拉方程为

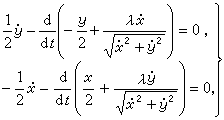(13)

解之可得曲线形状为圆周。这一答案是由雅各布第一·伯努利于1701年得到的。在条件(11)之下求泛函极值的问题常冠以等周问题的名字。

另一类条件极值问题中函数y，z服从一个约束

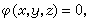(14)

而求泛函

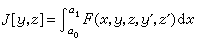(15)

的极值，这时存在函数λ(n)使在极值曲线上和函数

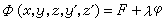　(16)

相应的关于y和z的欧拉方程(8)成立。

这类条件极值的典型问题是测地线的问题。在曲面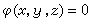上求连结两点A(x₀，y₀，z₀)和B(x₁，y₁，z₁)的最短弧Г：y=y(x)，z=z(x)，弧长

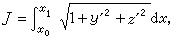
由上述结果可断言测地线上每一点的主法线与曲面的法线重合。测地线问题由约翰第一·伯努利在1728年向欧拉提出。欧拉当年给出了曲面上测地线微分方程。

泛函极值的充分条件

使泛函的一阶变分为零的函数或等价地相应欧拉方程（和适当边界条件）的解称为泛函的稳定点。泛函的极值点必是稳定点，但反之未必成立，对数值变量的函数就已如此。变分法的第二个基本问题是寻找应该加在稳定点上的条件以保证它是极值点，此即极值点的充分条件。在稳定点这一条件之外再继续寻求一定个数的必要条件，然后再检验这些必要条件是否保证稳定点就是极值点。在函数极值问题中，ƒ在O处取极小值，必须O是稳定点，即ƒ┡(O)=0，并且二阶导数ƒ″(O)≥0，但显然ƒ″(O)=0不能保证O点是ƒ的极小值点，而严格不等式ƒ″(O)>0足以保证O是ƒ的极小值点，这正好与泛函极值相对应。

勒让德条件

仍以固定端点的泛函(1)的极小问题为例，限制在允许函数的一维空间y₀+tη（t为实数）上考虑泛函J，y₀是极小值点，η是任一端点为零的光滑函数，已知y₀满足δJ[y₀]=0，且使二阶变分

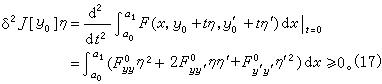
这里二阶变分的意义是当η 和η┡的绝对值都很小时，泛函 J[y]在稳定点y₀的增量J[y₀+η]- J[y]的二次主部。要使(17)成立，一个必要条件是

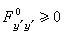。　　　　(18)

这里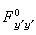是把稳定点代入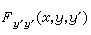所得的函数。条件 (18)称为勒让德条件。由A.-M.勒让德在1786年得到，翌年他领悟到这也只不过是个必要条件。建立充分条件的工作，50余年后由C.G.J.雅可比实现。雅可比条件设强化的勒让德条件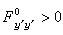成立，对二次变分(17)进行分部积分

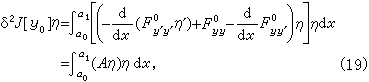
由常微分方程的特征值理论可知要(19)式对任意不恒等于零的函数η取正值的充分必要条件是二阶微分算子A的最小特征值为正数，或方程

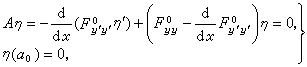　 (20)

的解在(α₀，α₁]内没有零点，除非η呏0。这一条件即所谓雅可比条件。

y与y₀差的绝对值的最大值叫做 y和y₀的零阶距离，y和y₀的零阶距离及y┡和y奿的零阶距离之和叫做 y和y₀的一阶距离。若对跟y₀的一阶距离小于某正数的一切函数y都有J[y₀]不大于J[y]，则说J在y₀取弱极小。勒让德条件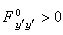和雅可比条件一起组成y₀是J[y]的弱极小的充分条件。

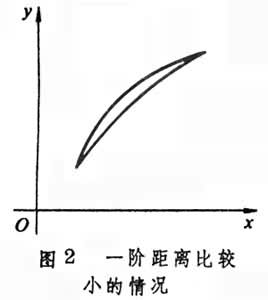
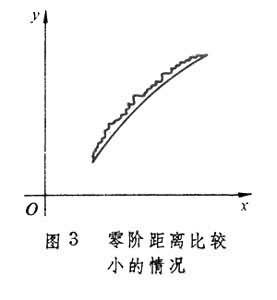
若对与y₀的零阶距离小于某个正数的一切函数y有J[y₀]不大于J[y]，则说y₀取强极小。

希尔伯特不变积分

由于与强极小点比较的函数为多，故应加更强的充分条件。仍以固定端点泛函(2)的极小值问题为例，设xy平面上一区域D的每一点(x，y)有且仅有一条稳定曲线通过，且过点(x，y)的稳定曲线的斜率记作v(x，y)，称v(x，y)为稳定曲线场的斜率函数。对过点P₀(α₀，b₀)， P₁(α₁，b₁)的所有曲线y=y(x)积分

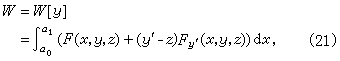
这个积分称为希尔伯特不变积分。由稳定曲线满足的欧拉方程和路径无关条件可以验证积分(21)不依赖于曲线y=y(x)。 (21)中的z=z(x，y(x))。

外尔斯特拉斯函数

(21)中的y=y₀(x)为连结点P₀和P₁的稳定曲线时z=z(x，y₀(x))=y奿(x)，故

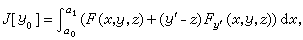
于是对任一连结P₀和P₁的曲线y有

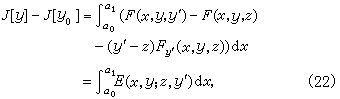
式中 E (x，y;z，y┡) ＝ F(x，y，y┡)-F(x，y，z)-(y┡-z) F_y┡(x，y，z)由泰勒公式易得，叫做外尔斯特拉斯函数。

强极值的充分条件

若有一围绕稳定曲线y₀=y₀(x)的稳定曲线场，且x，y，z独立变化时

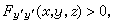(23)

y₀必为极小函数。务必注意(23)和勒让德条件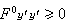的巨大区别。

由于欧拉方程中最高阶导数项的系数是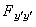，为使方程有二次连续可微的解y，就需要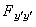在相应区域上永不为零，于是它不改变正负号，从而(23)本质上并非新的额外条件。满足 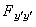恒不为零这一条件的问题称为正则问题。正则问题的稳定曲线总给出极小值或极大值，视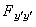的符号为正或负而定，恰如在一元函数的情形在稳定点的二阶导数不为零和在多元函数的情形在稳定点的二阶微分为正定或负定二次型一样。条件(23)是K.（T.W.）外尔斯特拉斯于1879年获得的，在1900年D.希尔伯特利用他的不变积分理论给这一充分条件以大大简化的证明。

数学物理与变分法

物理学中泛函极值问题的提出促进了变分学的建立和发展，而变分学的理论成果则不断渗透到物理学中。

物理学中的变分原理

P.de费马从欧几里得确立的光的反射定律出发提出了光的最小时间原理：光线永远沿用时最短的路径传播。他原先怀疑光的折射定律，但在1661年费马发现从他的光的最小时间原理能够推导出折射定律，不仅消除了早先的怀疑，而且更加坚信他的原理。拉格朗日把变分法用到动力学上。他引进广义坐标q₁，q₂，…，q_n，假定动能T是 q=(q₁，q₂，…，q_n)和孭=(孭₁，孭₂，…，孭_n)的函数，孭表示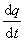。他又假定力有位势V，V是q的函数，又假定T+V是常量，即能量守恒定律成立，令L=T-V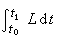，称为作用量，拉格朗日的最小作用原理是说真实的运动使作用量取极小值。通过欧拉方程，拉格朗日建立他的运动方程，据此推出了力学的主要定律，并解决了一些新的问题。这些工作都记载在他在1788年出版的《分析力学》一书中。

W.R.哈密顿把 P.-L.M.de莫佩蒂、欧拉、拉格朗日等人的最小作用原理推进到一个崭新的阶段，提出稳定作用原理。他在1834～1835年的两篇论文里，重新考虑S.-D.泊松引进的以拉格朗日命名的函数L=T-V，这里动能和势能皆可为时间t，广义坐标q和广义速度孭的函数，不必假定能量守恒定律，定义作用量

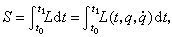(24)

式中 q在起始和终止时刻 t₀和t₁时分别取定值P₀和P₁，哈密顿稳定作用原理断言，真实运动是使作用稳定的运动。泛函(24)的稳定函数所满足的欧拉方程便是哈密顿方程，后来雅可比引进适当的变量替换而得到哈密顿－雅可比方程。由哈密顿的稳定作用原理可以推演出各种力学问题的运动规律。这一巨大成功鼓舞人们竞相在其他数学物理分支，如弹性力学、电磁理论、相对论、量子理论中求得类似的变分原理。

数学物理问题的变分解法

数学物理中大量存在着的变分原理从一个侧面反映了客观世界的统一性，也体现了人们建立统一的物理规律的渴望。一般说来变分原理对已有的理论是锦上添花。另一方面变分法对解许多实际物理问题也提供了切实可行的方法，例如可用变分法解振动系统的本征频率问题、散射问题等。基于变分原理还建立了偏微分方程的弱解的L²理论及相应的有限元解法和其他直接解法。

大范围变分法

18世纪是变分法的草创时期，建立了极值应满足的欧拉方程并据此解决了大量具体问题。19世纪人们把变分法广泛应用到数学物理中去，建立了极值函数的充分条件。20世纪伊始，希尔伯特在巴黎国际数学家大会讲演中提到的23个著名数学问题中就有三个与变分法有关，变分法的思想贯穿了R.库朗和希尔伯特所著的《数学物理方法》一书。而H.M.莫尔斯的大范围变分法则是20世纪变分法发展的标志(见莫尔斯理论)。