判定问题

[拼音]：panding wenti

[外文]：decision problem

判定所谓“大量问题”是否具有算法解，或者是否存在能行的方法使得对该问题中的每一特例能在有限步内机械地判定它是否具有某种性质（如是否真、是否可满足或是否有解等，随大量问题本身的性质而定）的问题。大量问题是与单个问题相对立的，它一般由无穷多个具有某种共性的单个问题组成。

上述“是否有算法解”，“是否存在能行的方法”的说法中的“是”，指有算法解或有能行的方法，这是不成问题的，因为凭人们的直观至少在理论上总可以判断一个解或一种方法是算法解或是能行的方法，尽管有时它很长而且很复杂；但对其中的“否”即不存在算法解或不存在能行的方法，则问题要麻烦得多。这要求要有精确的“算法”概念或精确的“能行性理论”概念。后两者在30年代才建立和发展起来，并成了“递归论”的基础部分。有了精确算法概念之后，随即发现许多长期悬而未决的大量问题不存在算法解，或者说是算法不可解的（根据丘奇论题，有时又说是递归不可解的），或者说该问题是不可判定的。其中最著名的有：

（1）狭谓词演算（也称一阶逻辑、一阶函项演算等）公式的可满足性的判定问题（A.丘奇，1936；A.M.图灵，1937）；

（2）群的字问题（∏.С.诺维科夫，1955；W.W.布恩，1959）；

（3）希尔伯特第10问题。

上述问题①就是希尔伯特所谓的“判定问题”。希尔伯特称它是数理逻辑的基本问题或中心问题。如上所说，1936年已证明此问题不可解（指算法不可解）。但全体公式类的不可解并不蕴涵其子类的不可解性。事实上狭谓词演算公式集的许多子类是有算法解的；当然也同样有许多子类（特别是所谓“归约类”）是不可解的。不妨把这方面的判定问题即由希尔伯特的“判定问题”所引伸出来的问题称为“狭义的判定问题”，并把对于一般的大量问题的相应问题笼统地叫作“判定问题”。

狭义判定问题

狭谓词演算公式的最简单而且最著名的可判定子类是全体只含一目谓词的公式类（L.勒文海姆，1915；A.T.斯科朗，1919；H.伯赫曼，1922），以及如下的两个前束类：

（1）具有前束彐…彐凬…凬的前束公式类（P.贝尔奈斯、M.S.芬克尔，1928）；

（2）具有前束彐…彐凬凬彐…彐的前束公式类（K.哥德尔，1932；L.卡尔马，1933；K.许特，1934）。

在讨论一阶逻辑的不可解公式类之前先介绍“归约类”的概念。简单地说，它们是这样的一些公式类，使得全体公式的判定问题能够能行地化归为这些类的判定问题。这方面最早和最简单的情形是只包含二目谓词变元的公式类(勒文海姆，1915)以及具有前束凬…凬彐…彐的前束公式类（斯科朗，1920）。

由丘奇和图灵的结果推出一切归约类均为不可判定的。图灵的证明是十分直截了当的。他用一阶逻辑中的公式对图灵机进行编码，由此由图灵机停机问题的不可解性便推出一阶逻辑的不可判定性。

归约法和编码法仍是证明一阶逻辑公式类不可判定性的两个主要方法，利用归约法可以证明如下公式类的不可判定性：

（3）具有前束凬凬凬彐的前束公式类（J.苏拉尼，1950）。

利用对“铺砖问题”进行编码可证如下公式类的不可判定性：

（4）具有前束凬彐凬的前束公式类（A.S.卡尔，E.F.莫尔和王浩，1962）。

（3）和④中的公式类都是归约类，而且可以看出公式类③为归约类一事可以容易地由④中公式类的归约性推出。不仅如此，有了④后许多有趣的归约类都能十分容易地得到。

综合①～④，如果不考虑等词，则有如下结果，它表明对前束公式类而言可解与不可解的问题已经完全解决。

给定任何量词串Q₁x₁，Q₂x₂，…，Q_kx_k，由此量词串所确定的前束类是一个关于可满足性的归约类，当且仅当该量词串包含凬彐凬或凬凬凬彐作为保持顺序而不一定相连结的子串。每个不是归约类的前束类都是可判定的。

如果单考虑公式中谓词的目数和个数，则有如下结果，它在这方面可能是最好的了。

（5）一切只含惟一的二目谓词变元R的公式的集是归约类（卡尔马，1936）。

狭义判定问题还有许多问题没有论及。主要是未讨论前束公式的母式的真值函数形式以及出现在原子子公式中的个体变元的顺序等。

关于狭义判定问题的另一个重要结果，是由Б.Α.特拉赫坚布罗特于1950年证明的，即一阶逻辑中公式是否在一有穷个体域上可满足是不可判定的。

一般大量问题的判定问题

又分为一阶(或初等)理论的判定问题和其他数学判定问题。前者是指给了一个形式理论，要求判定属于相应语言的任一语句σ能否由该理论推出，或等价地，σ是否在该理论的一切模型上为真。例如，G.皮亚诺算术理论PA和公理集合论中的ZF系统都是不可判定的一阶理论的例子，而实闭有序域或代数封闭域的一阶理论则是可判定的一阶理论的两个例子。后者的例子也很多，如群的字问题（M.德肯，1911），丢番图方程可解性的判定问题（希尔伯特第10问题，1900）等。

可判定理论的例子

以下对一数学结构或模型ц₀，令Th(ц)表一切在ц上真的语句组成的完备理论。

（1）Th(＜ω，≤＞)（C.H.兰福德，1927；其中ω表全部自然数的集合）；

（2）Th(＜Q，≤＞)（兰福德，1927；其中Q表全体有理数的集合）；

（3）Th(＜ω，+＞)，（M.普雷斯伯格，1929）；

（4）Th(＜R，0，1，+，·，≤，＞)（A.塔尔斯基，1948;其中R表一切实数的集合）；

（5）代数封闭域的初等理论（塔尔斯基，1948）；

（6）交换群的初等理论（W.什米莱夫，1954）；

（7）布尔代数的初等理论（塔尔斯基，1940）。

以上诸理论的可判定性均可用消去量词方法得到，而①～⑤情形的可判定性亦可用模型论方法得到。用模型论方法可证明其可判定性的理论还有：

（8）P 进位域的初等理论（J.阿克斯和 S.B.科琴，1965～1966）；

（9）有限域的初等理论（阿克斯，1968）；

（10） 线性（全）序集的初等理论（A.埃伦托伊希特，1959）。

情形（8）否定了长期悬而未决的如下猜想：除实闭域和代数封闭域外，没有其他可判定的无限域。

证明理论的可判定性的方法除上面提到的消去量词和模型论方法外还有解释方法。情形（3）的可判定性就可用解释方法证明。不过用解释方法证明为可判定的理论大都是二阶的。

不可判定的理论

丘奇1936年用哥德尔1931年证明不完备性定理的想法首先证明了皮亚诺算术理论PA（及其若干子理论）为不可判定的。J.B.罗塞同年证明PA的任何无矛盾扩张均为不可判定的。塔尔斯基称这样的理论为本质不可判定理论。这种证明不可判定性的方法叫做直接方法。用直接方法能证明其不可判定性的理论应当充分强，使得数论的推理工具能在其中发展。还有一种间接方法，即归约方法，其要点在于，把一理论T₁的判定问题归约到一不可判定的理论T₂，由此证明T₁亦为不可判定的。这里又分两种情形：

（1）证明T₁由T₂删去有限条公理而得，丘奇正是用这一方法于1936年证明一阶逻辑为不可判定的。

（2）证明某一本质不可判定理论T₂可以在T₁中解释。采用PA作为本质不可判定理论T₂，可证明各种公理集合论系统为不可判定的。

上述间接方法的适用范围仍是有限的。还有一种广义间接方法，它把上一方法中的两种情形①、②的某些特点结合起来。这就是说，为了证明理论T₁不可判定，只须把一有穷可公理化的本质不可判定理论T₂在T₁的某一无矛盾扩张中解释即可。此种理论T₂自然不能沿用PA，因后者是不可有穷公理化的。下面的鲁宾孙系统Q适合一切要求，其公理只有7条

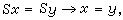
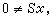
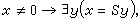
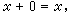
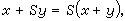
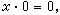
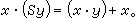
用这种广义间接方法已证明：群、环、域和格的初等理论均是不可判定的。还可证明，各种类型的群、环、域和格的初等理论的不可判定性。R.M.鲁宾孙还用这些方法证明了许多特殊环R的完备初等理论Th(R)为不可判定的。此种环称为不可判定的环。

不可解的问题

大批不可解的问题属于组合判定问题，其中较有意义的是半群的字问题(A.图埃，1914)和群的字问题。前一问题已证明为不可解的（E.L.波斯特，1947；Α.Α.马尔可夫，1949）。群的字问题则要困难得多。如前面所说它的不可解性已由诺维科夫和布恩在50年代相互独立地证明。值得指出的是G.希格曼1961年证明了如下定理。

希格曼定理

一个群是递归可表示的当且仅当它同构于一有限呈示群的子群。

这个定理表明递归可表示这一递归论概念等价于一纯代数概念。群的字问题的不可解性是它的一个容易的推论。

另外两个有名的不可解问题是分属于拓扑学和数论的问题：

（1）1958年证明维数≥4的流形同胚问题不可解（二维情形已由（G.F.）B.黎曼解决；三维流形的问题尚未解决）；

（2）关于丢番图方程可解性的判定问题(即希尔伯特第10问题)已于1970年最后否定地解决。

无论是狭义判定问题还是一般判定问题，在可解的情形有一个算法复杂性或可行性问题，对不可解的问题，则有一个不可解度的问题。

参考书目

1. A.Tarski，et al.，Undecidable Theories，Humanities Press，New York，1953.
2. J.Barwise，ed.，Handboo噚 of MatheMatical Logic，Horth Holland，Amsterdam，1977.
3. B.Dreben and W.D.Goldtarb，The Decision Problem Solvable Classes of Quantificational Formulas，Addison Wesley，Reading，Mass.，1979.