生物统计

[拼音]：shengwu tongji

[外文]：biostatistics，biometry，biometrics

应用于生物学中的数理统计方法。即用数理统计的原理和方法，分析和解释生物界的种种现象和数据资料，以求把握其本质和规律性。

发展简况

最早提出生物统计思想的是比利时数学家L.A.J.凯特莱，他试图把统计学的理论应用于解决生物学、医学和社会学中的问题。1866年，G.J.孟德尔揭示了遗传的基本规律，这是最早运用数理统计于生物实验的一个成功的范例（见孟德尔定律）。1889年，F.高尔顿在《自然的遗传》一书中，通过对人体身高的研究指出，子代的身高不仅与亲代的身高相关，而且有向平均值“回归”的趋势，由此提出了“回归”和“相关”的概念和算法，从而奠定了生物统计的基础。高尔顿的学生K.皮尔逊进一步把统计学应用于生物研究，提出了实际测定数与理论预期数之间的偏离度指数即卡方差(x²)的概念和算法，这在属性的统计分析上起了重要作用。1899年，他创办了《生物统计》杂志，还建立了一所数理统计学校。他的学生W.S.戈塞特对样本标准差作了许多研究，并于1908年以“Student”的笔名将t-检验法发表于《生物统计》杂志上。此后，t-检验法就成了生物统计学中的基本工具之一。英国数学家R.A.费希尔指出，只注意事后的数据分析是不够的，事先必须作好实验设计。他使实验设计成了生物统计的一个分支。他的学生G.W.斯奈迪格把变异来源不同的均方比值称为F值，并指出当F值大于理论上 5％概率水准的F值时，该项变异来源的必然性效应就从偶然性变量中分析出来了，这就是“方差分析法”。上述这些方法对于农业科学、生物学特别是遗传学的研究，起了重大的推动作用，20世纪20年代以来，各种数理统计方法陆续创立，它们在实验室、田间、饲养和临床实验中得到广泛应用并日益扩大到整个工业界。70年代，随着计算机的普及，使本来由于计算量过大而不得不放弃的统计方法又获得了新的生命力，应用更为广泛，并在现代科技中占有十分重要的地位。

个体与总体参数

一个观测对象(如一个7岁男孩)的某些性状（如身高等）的量度结果，称为一个个体。来源相同的各个个体(如各个 7岁男孩的身高值)之间的差异称为个体变异。总体是通过统计所欲了解的对象，其中的个体可以是有限的也可以是无限的。观测数据可以是计数的（离散的）（如单位面积中的昆虫数），也可以是计量的（如身高、体重、血压、肺活量等）。总体最基本的参数有两类：表示水平的称为位置参数或型值，如平均数、中位数、率等；反映个体差异大小的称为分散度参数，如标准差、极差等。总体参数是一个客观存在但通常却又是未知的常数。只能用样本去估计它。这样做自然会有误差。

样本平均数，即

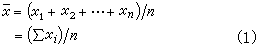
其中x_i表示第 i个个体的观测值；n为样本中的个体数，称为样本大小；∑为求和号，∑x表示x的合计。凡是从样本计算出来的数值都称为统计量，它是对相应的总体值的一种估计。例如塣是总体均数μ 的一种估计。若总体均数塣正好等于μ，则称塣为μ 的无偏估计，意谓用塣估计μ虽有误差但平均来说是无偏的。此时又称μ 为 塣的期望，记作。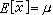

率

反映事物或现象出现的机会或频度，常用百分率或小数表示。如:感染率、死亡率、男婴率等。若以P代表阳性率，则阴性率Q＝1-P。若将男婴记作x＝1，女婴记作x＝0，则n个婴儿的性别指标的均数塣＝(∑x/n＝P就是男婴率。可见，率可以看成是个体取值为1或0的计数数据的均数。这种样本的率P也是对应的总体率P的无偏估计。总体的率又称为概率。

中位数

是数据按大小排列后位于中央的数值。对于分布不对称的指标（如机体内、外环境中的有害物质浓度等）往往会有少数特大值，此时，中位数比均数更具代表性，也更稳定。当n为偶数时，则取中央两数的均数。

众数

即最常出现的数值。如正常妊娠天数的众数为280天。

极差

即最大值与最小值之差。是用于表示数据分散度的简单指标。

方差

比极差更全面地反映个体差异的大小。若总体中有N个个体，则总体的方差为

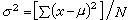　　　　　　 (2)

样本方差

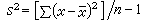　　　　　 (3)

是总体方差的无偏估计。若(3)式的分母改用n，就不是无偏估计。n-1是自由度：样本中有n个独立的观测指标x，它们都是随机变量，它们对于总体均数的离差平方和∑(x-μ)²，是n个独立随机变量之和，称为有n个自由度；而(3)式中的∑(x-塣)²，是用塣代替了μ，等于对n个x的值加了一个限制，即∑x必须等于n塣，换言之，∑(x－塣)²只相当于n-1个独立的随机变量之和，所以它只有n-1个自由度。一般地说，对统计量每加上一种限制就用去了一个自由度。为了运算上的方便，离均差平方和有时也记作：

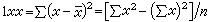　　　 (4)

标准差

是方差的平方根。它和观测值有相同的单位。是最常用的表示数据分散程度的指标。对于正态分布的数据，它的用处尤大。样本标准差s是对总体标准差σ的一种估计。s的值可在有统计功能的计算器上直接得出。计算s值的功能键常用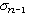表示。

变异系数

即

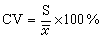　　　　　　　 (5)

它是不受单位影响的量，可用于比较两种单位不同的指标(如生物体的长度与重量)的个体变异大小。例如，三只小白鼠的体重x＝22，24，27（克）。它们的均数

塣＝(22+24+27)/3＝24.3（克）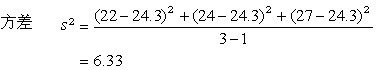

标准差

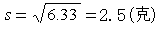
变异系数

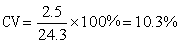
极差　Δx＝27-22＝5（克）。中位数是24克。

概率

表示客观事物可能发生的程度。它是实际观察到的率(如男婴率)的总体均值或期望值。它的通用符号是P。常用小数或分数表示其大小。例如用0《P《1表示概率的取值范围为0～1:假定P(男婴)＝22/43＝0.512表示生男婴的概率为22/43或0.512，即略大于1／2。这一理论值是根据反复多次的大样本统计结果归纳出来的。概率可以从量的方面来说明总体的性质。所谓“小概率事件”是指实际上不大可能发生的事件。

为充分地了解一个总体，就须知道个体的取值范围，以及出现的各种可能值的概率，即概率分布，简称分布。

正态分布

一种理想的对称型分布。有些生物学指标远非正态分布，而是呈左右不对称的所谓偏态，但当样本增大时，它们的均数却趋向正态分布。这一性质有重要的实用价值。

直方图

一种根据频数表绘制的图，它以横轴上的长方形的面积表示各组的频数，长方形在横轴上的边长相当于组距（图1）。

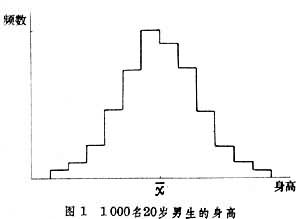
如果一步步地缩小直方图的组距，同时增大样本含量，最终将要趋于图2那样的极限。在图2中，曲线以下横轴以上的面积表示概率，这种曲线称为“(概率)分布曲线”。

正态分布具有以下性质：以总体均数μ为中心，在中心处的分布曲线最高；两侧与μ 距离相等的对称区间的上方有相同的面积(概率)；与μ 相距愈远的区间的概率愈小；可以用μ与σ(总体标准差)这两个参数来描述整个分布（图3）。

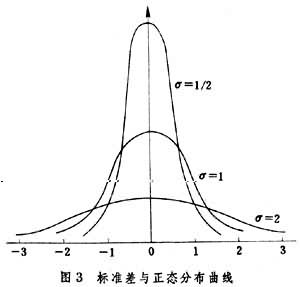
只要知道了μ 和σ，则个体落入任何区间的概率均可从（统计学书上）事先算好的正态分布表中查得。表1是这种表的一个摘要。

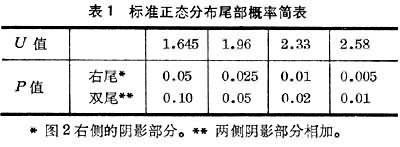标准正态分布

凡是正态分布的数据，均可通过减去均数并除以标准差而使之成为均数为0、标准差为1的标准正态分布。经过这种变换的指标记为U，

　　　　　(6)

x 遵从均数为μ 标准差为σ的正态分布，通常以简单的符号来表示:x～N(μ ，σ)。故可用U～N(0，1)表示“U遵从标准正态分布”。这种分布很常用，尤其是表1所列几个界限值。

当样本含量增大时，不论原始数据是不是正态分布，它的大多数统计指标均趋向正态分布，从而可以进一步化为标准正态分布，再根据μ 的界值来作出推断（表1）。

正常范围

生物界的正常范围常用于诊断、鉴别和分类。制定正常范围需要一些先决条件：原始数据必须来自同一总体；样本对总体的代表性要好；仪器、试剂和方法都没有偏性。理想的界限应有较高的灵敏度与特异度。前者是对异常者的识别率＝1-假阳性率；后者是对正常者的识别率＝1-假阴性率。当尚未掌握异常者的情况时，可暂将特异度定在0.95(即95％的正常者为此范围所覆盖)的水平；待掌握了异常者的数据分布后，再酌情修改界限以便兼顾灵敏度与特异度这两个方面。

抽样

为了估计总体的参数（如均数、率、标准差等）而从其中抽出一部分个体组成供分析的样本称为抽样。抽样方法应能防止主、客观因素造成偏性（即系统误差），保证样本对总体的代表性。简单随机抽样是以抽签或相当于抽签的方式从总体中抽取个体组成样本。其要点是：总体中每个个体被抽中的机会必须均等。系统抽样是将总体划分为时间或空间顺序相等的n个部分，再机械地取每一部分的第K个个体组成样本，K是一次随机抽定的。例如，欲抽查十分之一学生的成绩，可从0到9这10个整数中随机地抽定一个数，假设为3，则凡学生证号最后一个数是 3者均为被抽中的对象。分层抽样是事先将总体分为不同的层次（如地区、年龄、性别等），再分别从各层次中按适当比例抽样。用此法可以从层间差异较大的总体中获取代表性较好的样本。整群抽样是以群体为单位进行抽样，凡抽中的单位就全面调查。此法便于实施，但抽样误差较大，一般不可沿用基于简单随机抽样的普通公式计算抽样误差。此外，还可以分阶段地、混合地使用上述方法。如两阶段抽样、多阶段抽样、分层整群抽样、多阶段等概率抽样等。

用样本统计量去估计总体参数难免会有抽样误差，它的大小与个体变异（标准差）的大小成正比；与样本含量的平方根成反比。表示抽样误差大小的统计指标是标准误

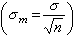
或代以统计量

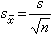　　　　　　　　　　(7)

相当于将每一个样本(设想有许多来自同一总体的样本)的均数塣（或率P）看成为一个个体时的标准差，它反映了取自同一总体的不同样本之间的差异。(7)式适用于简单随机抽样和系统抽样。其他几种抽样方法的算式较繁。

差异的显著性

两个或两组数据相比，总会有或大或小的差异。问题是这种差异仅仅是抽样误差的反映呢还是由于它们来自不同的总体？即是否存在着实质性差异？用统计学的术语来说，就是要判断数据间的差异是否“显著”。用统计方法来推断差异的性质称为差异的显著性检验。显著性检验的方法很多，基本步骤大体如下：先假定数据均来自同一总体，即假设要比较的数据并无实质性差异，称为零假设；根据原始数据计算因抽样误差而出现此种程度差异的概率P；若P甚小，则根据“小概率事件实际上不大可能发生”这一原理否定零假设，认为“差异显著”，即这种差异从统计学的角度来看是有意义的；反之，若P不算小，就不否定零假设，认为“差异不显著”，即不能排除抽样误差范围内的波动。正确地运用显著性检验，可使实验或调查的结论建立在更科学、稳妥的基础之上，避免简单化和绝对化。

显著性水准

概率的大小只能相对而言，在生物学数据的差异显著性检验中，已习惯用α＝0.05为小概率的上限。有时，为严格起见，也规定α＝0.01。称α为显著性水准，它是当零假设正确时却错误地将其否定（第Ⅰ类错误）的概率。但也不是α 定得愈小愈好。倘若零假设是不对的却未能否定，它(第Ⅱ类错误)的概率β 将因α规定得愈小而愈大。增大样本可以减小出现第Ⅰ或第Ⅱ类错误的概率。

两个计数数据的比较

最简单的差异显著性检验是比较按零假设系“来自同一总体”的两个计数a与b。

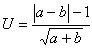　　　　　　　　 (8)

U服从标准正态分布。换言之，U>1.96的概率P<0.05（表1）。

例如，用“714”试治喘息型气管炎，与用氨茶碱进行比较：在每名患者身上交替使用这两种药各一疗程。半数患者先服甲药，另一半先服乙药。结果16名患者用氨茶碱效果较好(a＝16)，5名用“714”较好(b＝5)。

将上述结果代入(8)式

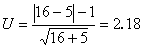
因U>1.96，P<0.05，故否定零假设，因此可以认为两药的疗效并不相同，即“714”的疗效不及氨茶碱。

凡用标准正态分布统计量U进行的显著性检验，均可称为U检验。

两个均数的比较

也可用U检验：

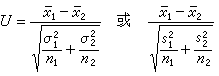　　　　　(9)

其中塣₁、s₁和n₁分别表示第1个样本的均值、标准和含量，余类推。σ²为总体方差，通常是未知的，故常用右边的近似式。当两样本的含量 n¹＋n₂＝n＜25时，(9)式的近似程度欠佳，最好用t检验。

t检验是根据统计量t的概率分布(称为t分布，见表2而进行的显著性检验。

比较两个均数时，

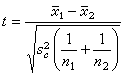　　　　　　　(10)

其中s娿为合并的方差，即

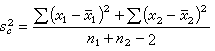
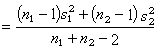　　　　　　 (11)

其中x₁表示第1个样本中的数据，x₂表示第2个样本中的数据，其余符号意义同前。自由度υ＝n₁+n₁-2。用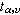表示显著性水准为α、自由度为υ的t临界值，可从表 3中查得。若按(10)式算得的t的绝对值大于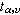，则P<d，有显著性差异。

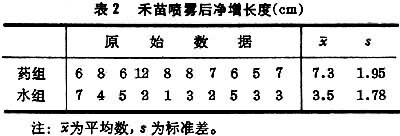
例如，在一块小区田里选20兜长势均匀的禾苗作试验，随机抽取其中10兜喷以粗制“920”溶液，其余喷水作对照。三日后，测量禾苗净增长度，结果如表2。

由(11)式

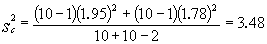
代入(10)式

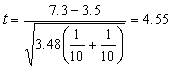
查表3，当α＝0.01，υ＝10+10-2=18，t_0.01，18=2.88；此例t＝4.55>2.88，p<0.01，有显著性差异。　结论：粗制“920”有加速禾苗生长的作用。

两个率的比较

当样本较大，以致两个样本的阳性数、阴性数都大于5时，可用U检验：

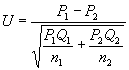
(12)P₁、Q₁和n₁，分别表示第1组的阳性率、阴性率和含量，余类推。若应用U检验的上述条件不能满足，可用近似程度较好的t检验：

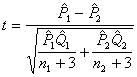　　　　　(13)

其中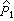=(a₁＋1)(n¹＋2)，a₁是第 1组的阳性数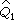，=1-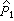，余类推。自由度υ＝n₁+n₂-2。

例如，甲组n₁＝23，其中两个呈“＋”反应，乙组n₂＝77，全为“-”反应。现在来检验差异的显著性。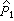=(2+1)/(23+2)=0.120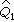，＝1－0.120＝0.880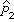；＝(0+1)／(77+2)＝0.013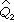，=1-0.013=0.987。代入(13) 式得t＝1.65，υ＝23+77-2＝98，接近100，由表3知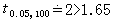，P>0.05，故无显著性差异。

置信限

由样本估计总体，难免会有抽样误差，这就产生了统计量的可信程度和可信范围的问题。如果我们将统计量塣（或P）看成为一个个体，塣的总体均数为μ，标准差为σ_m＝σ/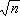；而且不论x的分布是否正态，只要n不是很小，塣就近似正态分布，亦即U＝(塣－μ)/σ_m近似标准正态分布。于是下式

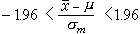　　　　　 (14)

成立的概率为0.95。用S_塣代替其中的σ_m，稍作变换，即得由样本统计量 塣和S_塣来估计总体参数 μ 的一个区间(范围)：

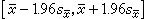　　　　　　 (15)

这一区间的实际计算值随样本而异，但它们覆盖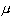的机会──称为置信水准──是95％，所以称(15)式为95％置信区间，它的上、下限就是置信限。

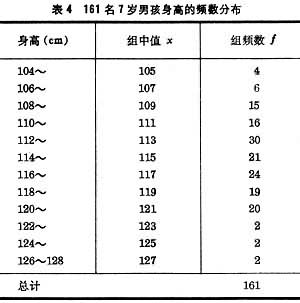
例如按表4中数据可算出161名7岁男孩的身高均值塣＝115.01(厘米)，标准差s＝4.63，标准误由(7)式得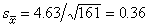。由 (15)式得 7岁男孩身高总体均数μ 的95％置信限为[114.95，115.73]。

两总体均数之差μ₁－μ₂的置信限可按下式计算：

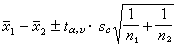　　　　　 (16)

式中符号意义同前。当置信水准(1-α)为95％时，α=0.05；υ＝n₁＋n₂-2;据此，从表2中即可查出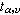的值。

方差分析

也是基本的统计分析方法之一，较常用于分析实验数据。用于检验多组均数间差异的显著性和多因素的单独效应与交互影响的显著性等。基本思路：正态分布数据的变差，可分为未能控制与未能解释的“误差”和来源明确与能够解释的“效应”这两大部分。后者还可以进一步划分成各种不同因素及其交互影响所引起的效应。

按一个因素的不同水平分组的数据结构：

观测值＝平均效应＋该水平（组）效应＋误差　(17)

当检验K组数据间的差异显著性时，零假设相当于“各组效应均为零”；当零假设被否定时备选假设相当于“在K种处理（水平）中至少有一种的效应不为零”。

一般用离均差平方和（记作SS）来衡量数据间的变异，再除以自由度(υ)则称为均方，记作MS＝SS/υ，它反映了平均的变异程度。设每组各有n个数据，则K组共有N＝nK个。它们的总变异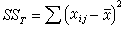，x_ij表示第i组的第j个数据;各组之间的变异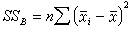，塣_i是第i组的均数；组内变异(即误差)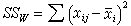。三者之间有以下关系：

SS_T＝SS_B＋SS_W　　　　　　　　(18)

它们的自由度也同样可加：

(nK-1)＝(K-1)+(nK-K)　　　　　　(19)

组间均方 MS_B＝SS_B/(K－1)与组内均方 MS_W＝SS_W/(nK－K)之比

F＝MS_B/MS_W　　　　　　　 (20)

可用来检验组间差异的显著性。F的界值可从F值表中查得。用于方差分析的软件可以打印出包含 F及相应的尾部概率P值的表格（表6）。

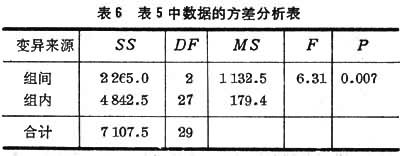
例如将 30名收缩压在200毫米汞柱左右的高血压患者随机分为3组，每组各用一种药物，一个疗程后测血压，结果如表5。

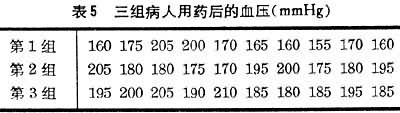
利用现成的计算机软件打印的结果如表6。表中P<0.01，表明组间有显著性差异。DF即自由变。

按两个因素分组的数据结构：

观测值＝均数＋行效应＋列效应＋交互影响＋误差 　　　　 (21)

其中“均数”指平均效应，行效应指按第1因素分组的组效应，列效应指按第2因素分组的组效应。交互影响的含义：当数据按两个以上的因素分组时，如果这些因素的效应并不是彼此独立的，即一个因素的效应随另一因素的水平不同而异，则称这两个因素之间存在着交互影响。

例如在三种病型的患者身上试用 4种药物后的血压改变如表7所示。其中每个数据代表一个病人的用药结果。

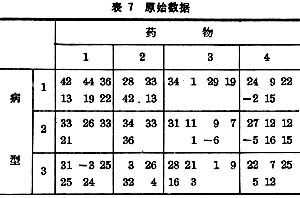
表8是计算机给出的结果。

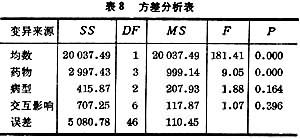
从P 值可以看出：三种病型之间无显著性差异；药物间有显著性差异；药物与病型的交互影响无显著性。“均数”除非来源于配对数据之差或两均数之差，一般都是有显著性的，即不为零。

只有进行了重复实验，即两因素的各种不同水平的搭配均有两个以上数据，才有可能算出交互影响项的变异。这是在设计时应该想到的。

上述内容不难推广到三个以上因素的方差分析。

理论的验证──x²检验

生物科学注重实验、调查。归纳得来的理论、演绎得来的假说，还须经过实践来验证。由于个体差异大是生物学数据的固有特点，所以这种验证也只能是统计的。

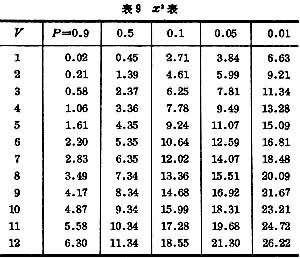
统计量x²

是 V个独立标准正态分布统计量的平方和，它的分布与自由度V有关(表9，图4)。

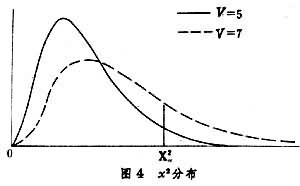
x²在生物学研究中用处很大，常用于衡量某种理论与实际计数的吻合性，或按两种指标分组的列联表的独立性。实际观察到的分配在表中每个小格里的计数数据，可以假定是服从泊松分布规律的数据──它的特点是方差等于平均数，且当样本不很小时，近似于正态分布。由此可以理解下列这个常用的基本公式。

x²＝　 (22)

其中的理论数可按欲检验的生物学理论或零假设计算，自由度 V＝x²中蕴含独立统计量的个数。对于普通的只有一行K格的单向表──1×K表，因受合计的约束，

V＝K-1

而双向的有r行c列的r×c表，则因受行合计与列合计的约束，

V＝(r－1)(c－1)

对计算结果的分析可参照差异的显著性检验。

例如番茄的真实紫茎、缺刻叶植株AACC与真实绿茎、马铃薯叶植株aacc杂交，子2代得如下结果（株数）:

紫茎缺刻叶　紫茎马铃薯叶　绿茎缺刻叶　绿茎马铃薯叶

247　　　　90　　　　　 83　　　　　34

上述观察频数是否与遗传学的独立分配定律的理论比例：9:3:3:1相符，可用x²分布来衡量实验观察结果与理论频数之间的吻合度。将上述理论比例改为构成比即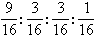：或0.5625:0.1875:0.1875:0.0625子2代总株数为247+90+83+34＝454；理论频数是总株数与构成比的乘积，故得255.375:85.125:85.125:28.375，代入(22)式：

x²＝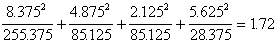

自由度V＝4-1＝3，查表9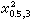，＝2.37>1.72，故P>0.5，高度吻合。衡量吻合度不能用小样。

列联表

即按两种指标分成r行c列的所谓r×c表，常用于衡量指标间的联系或独立性，为此亦可用(22)式。

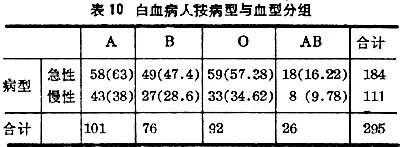
例如根据表10中数据分析血型与白血病病型间有无联系。零假设是“二者没有联系”。括号中数据是根据零假设计算的理论频数＝行合计×列合计÷总计。代入(22)式得x²＝1.84，V＝行数－1×列数－1＝（2-1）×(4-1)＝3。查表3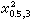，＝2.37＞1.84，P>0.5，故不能否定零假设。即不能认为血型与白血病病型有联系。

回归与相关

用来建立或明确两种指标之间的关系的统计技术。前者可用于分析一个变量受另一变量影响的程度；后者则用于分析两个对称或“平等”的指标之间的关联程度。

直线回归是用简单的直线方程尲=a+bx来拟合依变量y（尲表示它的估计值）受自变量x影响的情形。式中的a与b可以在有回归功能键的计算器上直接得出，但需按说明书将成对的观测数据(x，y)输入。计算程序的原理在于使 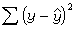极小化。若自变量不止一个，则有尲＝b₀＋b¹x¹＋b₂x₂＋…，称为多元回归，可用于预测、判别与指标的综合等。一般的微电脑常有计算多元回归系数b_i等的程序。

直线相关系数r=bS_x/S_y(其中b为回归系数，S_x、S_y分别为x与y的标准差)，其绝对值反映两个指标相关的程度。r的取值范围是-1到+1。它也可以在计算器上直接得出。

概率单位分析法

主要用于处理生物对化学或物理刺激的反应曲线。是一种以剂量的对数为自变量，以反应率的概率单位为依变量，从而使S型曲线直线化而便于分析的一种方法，可用于测定药物、毒物或物理因素对机体作用的强度和分析它们的联合作用。

无分布法

大多数统计分析方法都建立在“数据为正态分布”这一基本假定之上，而许多生物学数据远非正态分布，采用无分布法可以绕过这一困难。这类方法往往比较直观，而且计算简便。有时，一部分(或全部)观测结果并不能直接用数据表示，只能用反映大小或程度的等级或秩次表示。例如，观测结果是“－”，“±”，“+”及“++”以上，排序后的等级便是1，2，3，4……。许多很有效的无分布法就是基于数据或观测结果的大小顺序的。由于无分布法通常并不涉及数据分布的参数（如平均数），所以有时也称为非参数方法。

生存分析

许多生物现象的动态观察结果都比一次性的横断面观察更能说明问题。例如：恶性肿瘤患者接受手术治疗的效果，要看他们术后经过一段时间的生存率，或者有必要描绘出在不同条件下的生存率曲线（以时间为横轴，生存率为纵轴），以便进行分析与比较；器官移植的效果，要看异体器官在体内正常工作和不被排斥的时间等。生存分析的用途是广泛的。

多元分析

又称多指标或多变量分析，是对多个观测指标同时进行综合性分析，所以比普通的一元统计分析更为全面、有效。这是40年代就已出现的一系列好方法。由于涉及较深的数学知识和很复杂的计算，妨碍了它们的普及，随着计算机和统计软件包的日益完善，预料多元分析不久将会成为生物科学研究的常规武器。多重回归是指多个自变量和一个因变量的回归；而多元回归是指不止一个因变量的回归。但二者常被混淆使用。它们可用于预测、指标的综合或自变量的筛选。判别分析是利用形如多重回归方程的判别函数来进行个体种类的判断或诊断。聚类分析是将许多个体或指标按它们的相似程度来归类。对个体进行聚类称为Q型聚类;对指标进行聚类称为R型聚类。Q型聚类和判别分析是数量分类学的两种基本方法。趋势面是以地理上的经、纬度为自变量的高次方程，可用于绘制研究对象在地理上的分布密度的等高线图，亦可用于预测。主成分分析的目的在于将许多彼此相关的指标变换成少数几个彼此独立的综合指标，而且它们包含了原来那些指标的几乎全部统计信息。因子分析的计算程序与主成分分析类似，但它不是研究指标的变换，而是分析个体间的内在联系，此法为心理学家所首创，也可用于研究复杂的疾病。

统计模型

几乎所有的统计方法都有一个数学模型作为背景。除了上述方法之外，在生物科学研究中用处较大的还有：捉放捉模型，用于个体总数的估计；对数线性模型，用于多维列联表（即按多个指标分组的计数资料）的分析；Logit模型，既可用来同时排除多个混杂因素的影响，又可用于处理定量的混杂变量与危险因子。如果所有指标都是定性的，Logit模型就成了对数线性模型的一个特例。

参考书目

1. 杨纪珂等：《现代生物统计》，安徽教育出版社，合肥，1985。
2. 汤旦林：《医用统计基础》，人民卫生出版社，北京， 1989。
3. C.C.Li，Introduction to Experimental Statistics，McGraw-Hill Book Co.，New York，1964.
4. P.Armitage， Statistical　Methods　in　Medical Research，Blackwell Seientific Publications，Oxford，1977.

参考文章

• 什么叫医学统计学？医学统计学与统计学、卫生统计学、生物统计学有何联系与区别？统计学