[拼音]：youhuanliang de wuxuan yundong
[外文]：irrotational motion with circulation
无粘性不可压缩流体中一类重要的绕物体的平面无旋流动。这类流动的特点是，在流场中任取一围绕物体的封闭曲线，沿此曲线的速度环量不等于零。二维翼型的绕流就是有环量无旋运动的一例。
圆柱的有环量绕流是有环量无旋流动中最简单的一种情形。将均匀流和指向上游的偶极子流以及原点处强度为Γ的点涡叠加起来，可得到绕圆柱的流动。其复位势（见奇点分布法）为：
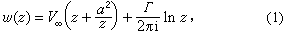
式中ω(z)为复位势；z为复变数;V∞为均匀流的速度；a为圆柱半径。容易看出，沿任一绕原点的封闭曲线的速度环量不等于零而等于一个有限值Γ。
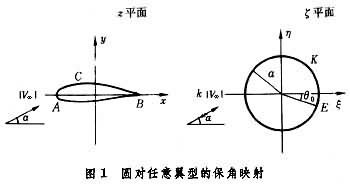
利用翼型到圆的保角映射函数， 可由圆柱有环量绕流问题的解直接写出翼型的有环量绕流问题的解。设ζ＝F(z)是一个单值的解析函数，它将任意剖面C外的区域单值且保角地映射到半径为a的圆K外的区域上去（图1），并且满足：
（1）∞点对应∞点；
（2）
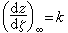，k为一个正实数。根据黎曼定理，函数ζ=F(z)是存在且唯一的。由ζ＝F(z)和圆柱有环量绕流问题的解(1)，可得任意翼型绕流问题的复位势：
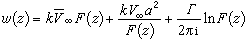， (2)
式中V∞和堸∞为无穷远处的复速度和共轭复速度。式中速度环量Γ的数值根据儒科夫斯基假设确定：后缘角点B是速度有限的一个驻点，流体平滑地流经翼型的上、下表面而从后缘流出。设角点B在ζ平面上对应的是圆上幅角为θ0的点E，由于E点是保角变换破坏点，满足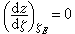
，于是根据
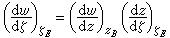和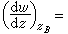
常数（儒科夫斯基假设），推出
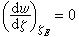，即ζ平面上E是驻点。据此可确定Γ的表达式：
Γ=－4πak│V∞│sin(α－θ0)，
式中│V∞│为无穷远处速度大小；α为来流攻角。
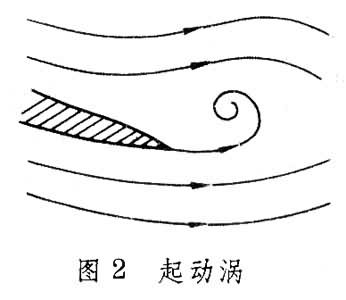
翼型一般是从静止起动的，根据开尔文定理，翼型引起的流体运动中涡量和速度环量应同静止流体一样处处为零；而根据儒科夫斯基假设计算出来的速度环量却是一个不等于零的有限值，且实际上存在的绕流图案总是使后缘角点成为驻点。原因是，当翼型刚在流体中起动时，后驻点不在角点而在上表面，流体从下表面绕过尖角进入上表面，形成大于180°角的流动。角点处速度无穷大，压力负无穷大，逆压梯度很大。物体表面生长起来的边界层承受不住这么大的逆压梯度，几乎立刻从后缘处分离形成起动涡（图2），使一部分流体发生旋转，从而产生了沿DCB的速度环量
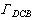（图 3）。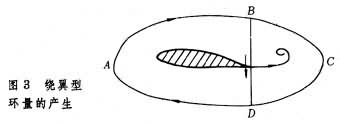
与此同时，在流体的另一部分产生反方向的旋转，这个反方向的转动以围绕翼型的环流形式出现，于是产生沿DAB的速度环量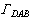
。因为无旋运动要求
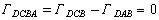，所以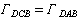
。绕翼型的反向环流会增加上表面的气流速度，使后驻点的位置向后推移。只要后驻点还在上表面，上述过程就会一直进行下去，流动继续分离，起动涡的强度和绕翼型的环量不断加大，后驻点位置不断后移，一直到后驻点移至角点处，机翼上下两边的气流在后缘平滑地相遇时不产生大于π 角的流动。此时出现后缘点速度有限的绕流图案。随着时间的推移，起动涡被气流冲到下游很远的地方，其全部能量逐渐被粘性所耗散，只留下绕翼型的一个固定的速度环量。这时流体内部仍然可以近似地看作是无旋运动。
