线性统计模型

[拼音]：xianxing tongji moxing

[外文]：linear statistical model

简称线性模型，是数理统计学中研究变量之间关系的一种模型，其中未知参数仅以线性形式出现。主要包括线性回归分析、方差分析和协方差分析。

线性回归模型是最简单的线性模型。以x1，x2，…，xk记自变量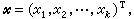，Y记因变量。有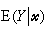=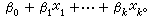式中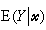是在给定自变量x值的条件下，因变量Y的条件均值，而β0，β1，…，βk是未知参数。这模型之所以被称之为线性模型，并不在于它相对于x1，x2，…，xk是线性的，而在于E(Y│尣)关于参数β0，β1，…，βk是线性的。因此，若ƒ1(尣)，ƒ2(尣)，…，ƒp(尣)是尣的p个已知函数，而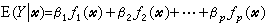关于参数β0，β1，…，βp依然是线性的，例如多项式回归（见回归分析）。若以Zi=ƒi(尣)(i=1，2，…，p)为新自变量，则可将模型变换为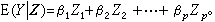因此可以一般地把线性模型的条件表述为

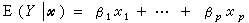　　　(1)

的形式。式中

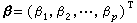
称为回归系数。若自变量尣取值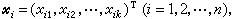得Y的观测值为Yi，并以εi记观测的随机误差，则得到n个关系式

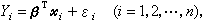　　　(2)

式中βT表示β的转置。(2)给出了线性统计模型的数据结构，而(2)只是一个理论模型。统计问题都是从(2)出发，故一般在谈到线性模型时常是指(2)。若记

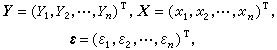
则可将(2)写成

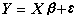， 　　 (3)

n×p矩阵 X称为设计矩阵。在回归分析问题中，自变量多是连续取值。因而 X的元素在一定范围内可以任意取值。在方差分析问题中， X的元素只取0，1为值，1，0分别表示某因素的某水平出现或不出现。在协方差分析问题中，二者兼而有之。

线性模型（3）的统计性质取决于对随机误差向量ε所作的假定。一般总假定 E(ε)=0，若再加上协方差矩阵（见矩）cov(ε)=σ2In（ In为n阶单位阵，σ2>0为未知的误差方差），则(3)称为高斯－马尔可夫模型。这是高斯在19世纪初引进的最小二乘法成为线性模型统计分析的重要工具，而俄国数学家Α.Α.马尔可夫在20世纪初完成了这种模型的奠基工作。若进一步假定ε服从n维正态分布N(0，σ2In)，则(3)称为正态线性模型。

模型(3)的统计问题，就是关于 β和σ2的统计推断问题。特别重要的是关于β的线性函数CTβ的估计和检验问题。关于β本身的估计，通常用最小二乘法，即寻找娕，使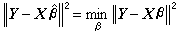（‖α‖表示向量α的欧氏长度）。可以证明娕是正规方程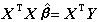的解，若行列式｜ XT X｜>0（称为满秩情况），方程有惟一解

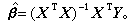
若｜ XT X｜=0（称为降秩情况），方程有解，但不惟一，可通过广义逆表示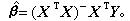：娕称为β的最小二乘估计（见点估计），它是Y的线性函数。对一般的参数的线性函数CTβ，若存在某一线性无偏估计αTY，则称它为可估函数。CTβ可估的充分必要条件是存在n维向量b，使C= XTb。β本身是否可估，取决于 XT X是否满秩。回归分析中的 XT X一般是满秩的，而方差分析则相反。

关于回归系数β的估计理论的一个基本结果，是高斯-马尔可夫定理:若(3)为高斯-马尔可夫模型而CTβ可估，则在CTβ的一切线性无偏估计中，CT娕是惟一的方差一致最小者。在正态模型下，可进一步证明，它是一切无偏估计(不限于线性)中方差一致最小者。若 X的秩为r(<n)，则误差方差σ2的一个无偏估计是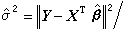 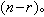在正态假定下，捛2是σ2的一致最小方差无偏估计。β的线性假设一般有形式H0:CTβ=0，在正态假设下，它可以用似然比检验法(见假设检验)去检验。所得似然比统计量(乘以适当常数因子)在H0成立之下服从中心F 分布。

在自变量之值可由实验者选定时，存在着设计问题，即怎样选择设计矩阵 X。在回归分析中，有一个主题叫回归设计，它讨论怎样选取适当的 X，使娕具有某种优良的性能。在方差分析中， X的选择更为重要，通常，实验设计法就是专指这种情况下 X的选择问题。

线性模型在实用上有重要意义。在理论方面，近年来也有不少新发展：在对β的估计上，发展了有偏估计、稳健估计、非参数估计及序贯估计等方法; β和σ2的估计的容许性问题得到了较深入的研究；另外，在大样本理论方面取得了广泛而深入的结果。

参考书目
  1. C.R.Rao，Linear Statistical Inference and Its Applications， 2nd ed.， John Wiley & Sons， New York， 1973.
  2. V.V.Fedorov，Theory of OptiMal Experiments， Academic Press， New York， 1972.
阅读全文