积分变换

[拼音]：jifen bianhuan

[外文]：integral transform

通过参变量积分将一个已知函数变为另一个函数。已知ƒ(x)，如果

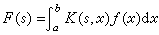
存在（α、b可为无穷），则称F(s)为ƒ(x)以K(s，x)为核的积分变换。

积分变换无论在数学理论或其应用中都是一种非常有用的工具。最重要的积分变换有傅里叶变换、拉普拉斯变换。由于不同应用的需要，还有其他一些积分变换，其中应用较为广泛的有梅林变换和汉克尔变换，它们都可通过傅里叶变换或拉普拉斯交换转化而来。

梅林变换

当K(s，x)=x^s_1，x>0，而ƒ(x)定义于[0，+∞)，函数

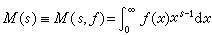　　　 (1)

称为ƒ(x)的梅林变换，式中s=σ+iτ为复数。M(s)的梅林反变换则定义为

(x>0)， (2)

这里积分是沿直线Res＝σ 进行的。

(1)式与(2)式在一定条件下互为反演公式。例如，设(1)绝对收敛，在任何有限区间上 ƒ(x)是有界变差的，且已规范化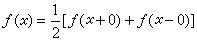：，则由(1)可推得(2)，在l²(0，∞)空间中也有类似结果。

若以M(s，ƒ′)表示ƒ′(x)的梅林变换， 则在一定条件下，有 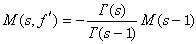。在一定条件下，还有下列梅林交换的卷积公式：

，

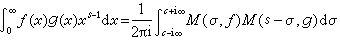式中с>Res。

一些简单函数的梅林变换(α ＞0)如表：

汉克尔变换

设J_γ(x)为у阶贝塞尔函数（见特殊函数），ƒ(x)定义于[0，+∞)，则称

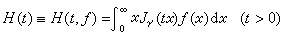(3)

为ƒ(x)的у阶汉克尔变换；而称

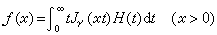　　 (4)

为h(t)的汉克尔反变换。有的作者代替(3)与(4)改用

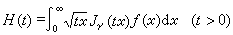
与

，

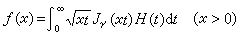效果是一样的。在一定条件下，(3)与(4)成为一对互逆公式，此外，还有

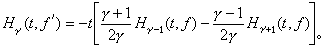
一些简单函数的汉克尔变换如表：

参考书目

1. A.Erdélyi， ed.，table of Integral Transforms，Vol. 1， McGraw-Hill， New York， 1954.
2. 特兰台尔著，潘德惠译：《数学物理中的积分变换》，高等教育出版社，北京，1959。(C.J.Tranter，Integral Transforms in MatheMatical Physics，2nd ed.，John Wiley & Sons， New York， 1956.)
3. D.V.Widder，An Introduction to Transform Theory，Academic Press， New York， 1972.