[拼音]：duanlie lixue
[外文]：fracture mechanics
断裂学科的一个分支，从构件内存在着宏观裂纹出发，应用线弹性力学和弹塑性力学方法进行分析和实验，从而对含裂纹的构件的安全性和寿命给出定量的或半定量的估算，提供构件的设计、验收、选材以及断裂韧性测定的理论基础。20世纪20年代，格里菲思(A.A.Griffith)试图解释玻璃的理论断裂强度和实测值之间的巨大分歧时，提出了由于固体内存在着裂纹，造成大的应力集中，使局部的裂纹扩展而造成断裂。他进一步从能量观点提出断裂判据：如果裂纹扩展所释放的弹性应变能足以提供裂纹扩展所需的表面能时，则裂纹扩展。但由于其数学-力学推导中没有考虑在裂纹前端的塑性变形功，所以结论仅能用于玻璃一类的脆性材料。以后欧文(G.R.Irwin)(1948)和奥罗万(E.Orowan)(1947)分别注意到，对于延性材料，局部的范性形变所作的功应该加入裂缝扩展的能量公式中；在裂缝扩展过程中，如果不供给足够的能量，则裂缝的扩展被抑止。1957年欧文运用韦斯特加德(Westergaard)应力函数，求出中心穿透裂纹板材双向受拉时的弹性力学解，这是运用力学方法认识复杂的断裂过程并走向工程实用的重要的一步(见形变和断裂)。根据对裂纹附近材料所假定的状态不同，分为线弹性断裂力学和弹塑性断裂力学，前者较为成熟。
线弹性断裂力学分析裂纹附近的应力状态的出发点是：裂纹前端的塑性区足够小，因此其周围材料的应力（σ）和应变（ε）的关系仍是线性的。由此来研究裂纹前端的应力场、应变场以及同裂纹扩展有关的能量关系，提出在这种条件下的裂纹扩展的判据。
构件中存在着裂纹并受到外载荷时，裂纹和载荷通常有三种组合形态：张开型（Ⅰ型）、滑开型(Ⅱ型)和撕开型（Ⅲ型），其中以Ⅰ型最危险，因此，即使是复合型的组合，也可以按照Ⅰ型来建立失稳判据。欧文求出了如附图所示的平板穿透裂纹双向受拉时的应力分布的解为：
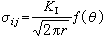(1)
式中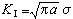
，KI叫作应力场强度因子；a为裂纹的长轴长度的一半;(r，θ)为所求点的极坐标；f(θ)为角θ的函数。
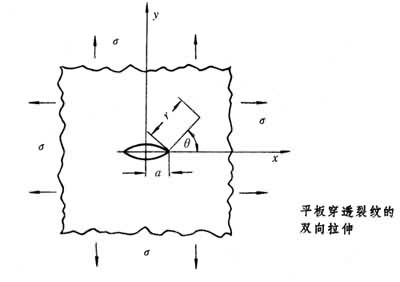
由上式再列入关于塑性区的修正，就可以求出Ⅰ型裂纹扩展时的能量释放率GI，有实用意义的情况是
平面应力时：
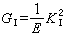(2)
平面应变时：
(3)
式中E 为材料的弹性模量；ν为材料的泊松比。
也可以研究更为普遍的、不限定裂纹为中心穿透的裂纹的情况，此时
(4)
式中α为与裂纹几何形状和加载方式有关的无量纲系数，中心穿透裂纹双向受拉时，α＝1；a为与断裂过程有关的裂纹特征尺寸。
由此可以得到断裂判据:当KI达到某个临界值KIc时，裂纹迅速扩展而致断裂，此时的应力记为σF，裂纹长度记为ac，则
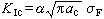(4a)
由此式可以测定各种材料的KIc，并求出适用于工程设计的断裂判据。KIc叫作平面应变时的材料断裂韧度，或简称为断裂韧度。但是应该指出，由于被其分析的基础决定，所得的结果只适用于在低应力下发生脆性断裂时的情况，一般为：σF≤0.6σs (5)
式中σF为材料的断裂应力，σs为屈服强度。
弹塑性断裂力学当裂纹前端的塑性区的相对尺寸较大时，线弹性关系不再适用，也就是不能再运用KI≥KIc作为断裂判据。此时，要用弹塑性力学处理裂纹体的断裂问题。在实验的基础上提出新的断裂韧性参量，得到新的断裂判据。目前比较成熟的判据有：
（1）应变判据 认为裂纹的顶端张开位移（crack opening displacement或简写为COD）达到临界值 (δc)时，裂纹失稳扩展，材料断裂。对于薄板双向受拉时的Ⅰ型穿透裂纹，可以导出以下关系：
(6)
展开：
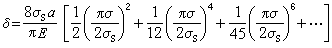(7)
对于低应力〔例如(5)式〕，可近似地只取无穷级数中第一项，则：
(8)
将(4)式代入，并考虑临界条件，则得到：
(9)
式中Kc为平面应力时的断裂韧度。
（2）能量释放率判据 当能量释放率GI达到临界值GIc时，断裂发生。在弹塑性条件下，确定了GI等值于某个沿围绕裂纹的团合回路的积分JI。可以证明JI值与积分路径无关，因而可把在特定条件下的实验测定临界值JIc用于弹塑性条件下的断裂判据。在线弹性条件下：JIc=GIc (10)
断裂力学讨论和处理了材料受力时裂纹的扩展条件和断裂判据，也可以用来分析在其他条件下，如疲劳、应力腐蚀（见应力腐蚀断裂和氢脆）等裂纹的形成和扩展；同时也就能够用于研究在各种条件下防止断裂的措施以及提高材料的断裂韧性的途径。
- 参考书目
- 肖纪美：《金属的韧性与韧化》，上海科学技术出版社，上海，1980。