[拼音]：xindao rongliang
[外文]：channel capacity
信道能无错误传送的最大信息率。对于只有一个信源和一个信宿的单用户信道，它是一个数，单位是比特每秒或比特每符号。它代表每秒或每个信道符号能传送的最大信息量，或者说小于这个数的信息率必能在此信道中无错误地传送。对于多用户信道，当信源和信宿都是两个时，它是平面上的一条封闭线，如图中的OC1ABC2O。坐标R1和R2分别是两个信源所能传送的信息率，也就是R1和R2落在这封闭线内部时能无错误地被传送。当有m个信源和信宿时，信道容量将是m 维空间中一个凸区域的外界“面”。
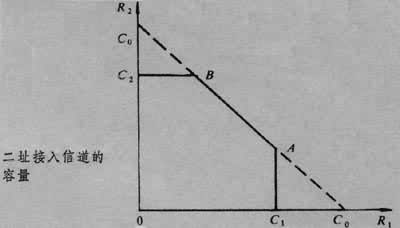
单用户信道容量
信道是由输入集A、输出集B和条件概率P(y│x)，y∈B，x∈A所规定的。当B是离散集时，归一性要求就是
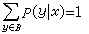
当B是连续集时，P(y│x)应理解为条件概率密度，上式就成为积分形式。如A和B都是离散集，信道所传送的信息率（每符号）就是输出符号和输入符号之间的互信息
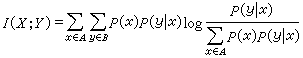
互信息与P(y│x)有关，也与输入符号的概率P(x)有关，后者可由改变编码器来变动。若能改变P(x)使I(X;Y)最大，就能充分利用信道传输信息的能力，这个最大值就称为单用户信道容量C，即
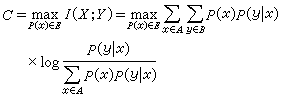
式中∑为所有允许的输入符号概率分布的集。
当A或B是连续集时，相应的概率应理解为概率密度，求和号应改为积分，其他都相仿。
多用户信道容量
多用户信道容量问题要复杂一些。以二址接入信道为例， 这种信道有两个输入 X2∈A1和X2∈A2，分别与两个信源联结，发送信息率分别为R1和R2；有一个输出Y，用它去提取这两个信源的信息。若信道的条件概率为P(y│x1，x2)，则
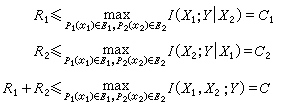
式中I(X1;Y│X2)为条件互信息，就是当X2已确知时从Y中获得的关于X1的信息； I（X2;Y│X1）的意义相仿；I(X1，X2;Y)为无条件互信息，就是从Y中获得的关于X1和X2的信息。E1和 E2分别为所有允许的输入符号的概率分布P1(x1)和P2(x2)的集。
当X1和X2相互独立时，这些条件互信息要比相应的无条件互信息大，因此两个信息率R1和R2的上界必为上面三个式子所限制。若调整P1(x1)和P2(x2)能使这些互信息都达到最大，就得到式中的C1，C2，C0。
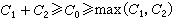
因此R1和R2的范围将如图中的一个截角四边形区域，其外围封闭线就是二址接入信道的容量上界。m址接入信道有类似的结果。更一般的多用户的情况还要复杂。
要使信道容量有确切的含义，尚须证明相应的编码定理，就是说当信息率低于信道容量时必存在一种编码方法，使之在信道中传输而不发生错误或错误可任意逼近于零。已经过严格证明的只有无记忆单用户信道和多用户信道中的某些多址接入信道和退化型广播信道。对某些有记忆信道，只能得到容量的上界和下界，确切容量尚不易规定。
计算
为了评价实际信道的利用率，应具体计算已给信道的容量。这是一个求最大值的问题。由于互信息对输入符号概率而言是凸函数，其极值将为最大值，因此这也就是求极值的问题。对于离散信道，P(x)是一组数，满足非负性和归一性等条件，可用拉格朗日乘子法求得条件极值。对于连续信道，P(x)是一函数，须用变分法求条件极值。但是对于大部分信道，这些方法常常不能得到显式的解，有时还会得到不允许的解，如求得的P(x)为负值等。为了工程目的，常把信道近似表示成某些易于解出容量的模式，如二元对称信道和高斯信道。这两种信道的容量分别为
C＝1-H(ε)（比特／符号）
和
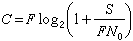（比特／秒）
后者当F→∞时为
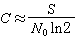（比特／符号）
二元对称信道的输入集和输出集都是二元集｛0，1｝，条件概率为P(0│0)＝P(1│1)＝1-ε，P(0│1)＝P(1│0)＝ε，是对称的。ε一般称为误码率或差错概率，而H(x)是熵函数，即
H(x)＝-xlog2x-(1-x)log2(1-x)
高斯信道的输入集和输出集都是实数集(-∞，∞)；干扰是加性正态白噪声或称为高斯白噪声，其单边功率谱密度为N0；信道是理想低通型的，通频带为F；S是允许的输入平均功率的上限。
对于其他信道的容量计算曾提出过一些方法，但都有较多的限制。比较通用的解法是迭代计算，可借助计算机得到较精确的结果。运算公式是
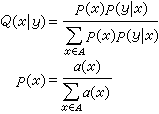
式中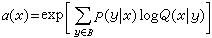 
可先任设一组P(x)，例如等概率分布。用前一式求得各Q（x│y），再用这些Q（x│y）代入后一式求得新的各P(x)；再用这些 P(x)代入前一式去求新的Q（x│y）；依此迭代下去，直到新的P(x)与前次的P(x)已经相等或差别小于允许值。用这时的P(x)去求I(X;Y)，就是所需的信道容量C。
这些迭代公式也是用求极值法获得的，只是引入了反条件概率Q（x│y）作为一组新的自变量，且发现当互信息I(X;Y)取极值时，Q(x│y)恰好满足作为反条件概率的条件。这种迭代运算最后一定收敛，而误差将按迭代次数N的倒数趋向于零。也就是当N→∞时，计算误差将为零而得到精确值。当N足够大时，误差就可小于允许值。此外，只要起始所设的P(x)满足概率的非负性和归一性条件，以后运算结果不会出现P(x)大于1或小于零的情况，因此所得结果总是有效的。
这一公式仅适用于离散无记忆信道，对P(x)除了非负性和归一性外没有其他限制。对于连续信道，只需把输入集和输出集离散化，就仍可用迭代公式来计算。当然如此形成的离散集，包含的元的数目越多，精度越高，计算将越繁。对于信息论中的其他量，如信息率失真函数，可靠性函数等，都可以用类似的方法得到的各种迭代公式来计算。