暂态频域分析

[拼音]：zantai pinyu fenxi

[外文]：frequency domain analysis of transient state

将电路或系统中的激励与响应用傅里叶级数或积分展开为频率不同的谐波之和，以分析稳态的方法对电路或系统的暂态过程及其特性进行分析。集总的线性时不变电路和系统的激励与响应的关系都由常系数线性微分方程来描述。如果施加以正弦形激励，如Asin(ωt+嫓)，或指数形激励，如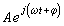，则其稳态响应一般亦呈同频率的正弦或指数形式。采用复数相量法，只需求解由电路方程所得复数方程组，就可以求得所需的响应。

暂态分析的目的是要研究在电路中施加激励后所出现的响应。对于线性时不变电路和系统，暂态的频域分析的基本思想是将激励展开为许多存在于 －∞<t<∞的正弦形或复数指数函数形的谐波，再根据线性电路的线性性质分别计算各谐波在电路中产生的谐波响应。这一计算与稳态分析一样，将所有的谐波的稳态响应相加即可得到所需的暂态响应。在激励是周期性时间函数的情况下，将激励展开为许多其频率是激励基波频率K倍(K是整数)的谐波之和，即为激励的傅里叶级数展开式，所得的响应亦表示为类似的级数形式。在激励是非周期时间函数的情况下，激励的展开式是频率连续分布在-∞<ω<∞的多不可数的谐波之和，这便是激励的傅里叶积分，所得的响应亦表示为类似的积分形式。

周期性时间信号的谐波分析

周期性连续时间信号是具有

g(t)=g(t+T₀)　　T₀≠0

性质的信号。满足上式的最小的T₀值称为此信号的周期，其频率为f₀。

满足狄里赫利条件的周期性时间信号可以用傅里叶级数展开为一系列频率为Kf₀（K＝整数）的简谐时间函数之和

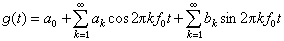　　(1)

式中

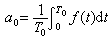
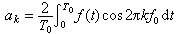
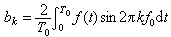
将式(1)中频率相同的正弦项、余弦项合并，即有

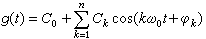　　　 (2)

其中

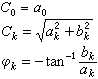
由(1)、(2)两式可知，周期性时间信号可表示为一系列谐波之和，这些谐波的频率为f₀的整倍数，C_k是频率为Kf₀的谐波的振幅，φ_k就是这一谐波的初相角。对一周期性信号可以作出它的各谐波振幅C_n、初相角φ_n与角频率ω的关系的图像，这种图像分别称为振幅谱和相位谱。

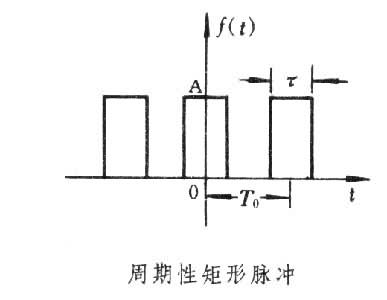
图中的周期性矩形脉冲的傅里叶级数展开式是

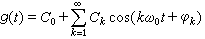
式中

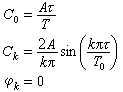非周期性时间信号的谐波分析

非周期性信号g(t)满足某些条件时，也可以展开为正弦形式的谐波的和。这时，由傅里叶级数的式中令T₀→∞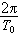，＝Δω→dω，可以得到傅里叶积分变换式

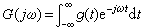　　 (3)

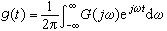　　 (4)

G(jω)为g(t)的傅里叶变换，g(t)则为G(jω)的傅里叶逆变换，记作

G(jω)=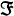[g(t)]　　 (5)

g(t)=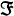^-1[G(jω)]　　 (6)

对式(4)可以作这样的解释:g(t)中频率为ω的简谐分量的复振幅以密度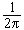G(jω)分布在ω轴上，将这些频率连续分布在(-∞，∞)上的所有谐波相加(积分)即得到g(t)。G(jω)是复数，它的模和幅角都是频率ω的函数。将G(jω)记作

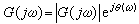　　　　(7)

式中|G(jω)|称作幅频函数，θ(ω)称为相频函数。对于实数值的信号有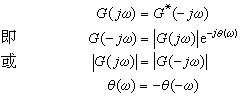即幅频函数是ω的偶函数，相频函数是ω的奇函数。

应用

集总的线性系统的输入激励与输出响应的关系可以用一常系数线性微分方程表示

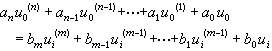　　 (8)

式中，u₀、u_i分别表示线性集总系统的输出量和输入量。带上标(K) 的量表示该量的K阶导数，例如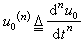等。对于形如e^jwt的激励，式(8)所表示的系统的传递函数为

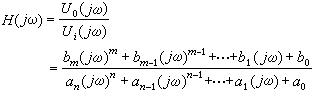对于任一形式的激励 u_i(t)作用于此系统所产生的响应u₀(t)，便可通过将u_i作傅里叶变换，得其频谱密度

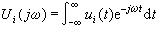
再应用叠加定理分别计算各频率为ω的指数形激励产生的响应，最后将这些不同频率的响应相加使得到u₀(t)。它便是系统在u_i(t)的作用下产生的零状态响应。这一结果可表示为下面的积分

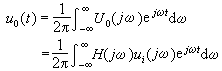
上式就是U₀(jω)的傅里叶反变换。在可以用解析的方法得到这一积分的通式的情况下，便可以得到u₀(t)的表达式。在许多情况下，是采用数值方法去求上式的数值解。这时要将积分限限制在一有限的范围，并作离散化的处理。由此发展起来的快速傅里叶变换技术，为解决这类问题提供了快速而有效的算法。