[拼音]:huilu dianliufa
[外文]:loop current method
以回路电流为求解对象的电路计算方法。回路电流是根据电流连续性原理假设的一种沿回路流动的电流。它一定满足KCL(见基尔霍夫定律)在一个支路数为b、节点数为n的电路内,沿所选定的(b-n+1)个独立回路流动的回路电流是独立的,所以用此法计算电路需要建立(b-n+1)个以回路电流为未知量的独立方程。 独立回路是指该回路中的KVL方程线性无关,在电路计算中通常取电路的基本回路(当电路是平面网络,则常取其网孔)作为独立电路(见网络拓扑)。
电路的回路方程回路电流法中列写方程的依据仍然是基尔霍夫定律和支路性质对支路电压和支路电流的约束。列写的具体步骤为:
(1)选定各支路电流和支路电压的参考方向,并对节点和支路进行编号;根据规定选出电路的一组基本回路并对它们进行编号;最后,规定各回路的绕行方向,同时把这个方向也作为回路电流的方向。
(2)对基本回路列写出 KVL方程。
(3)写出表达支路电流与回路电流之间关系的方程。这种方程亦称 KCL方程。
(4)写出各支路的支路方程。
(5)将第3步中的KCL方程代入第4步中的支路方程,消去支路电流后得出支路电压改由回路电流表达的新支路方程。
(6)将第 5步得到的新支路方程代入第2步的KVL方程,消去支路电压,得到的便是此法所需要的方程。按上述步骤得出的方程称为电路的回路方程。
具有l=b-n+1个基本回路的线性电路的回路方程的一般形式是
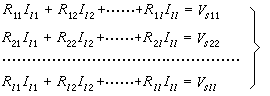 (1)
(1)
式中Rij(i=1,2,…,l)是回路i中的所有电阻之和,称为回路i的自电阻;Rij(i、j=1…l,i≠j)是回路i与回路j 所共有的电阻(互电阻),在回路电流Ii与电流Ij在共有支路中方向相反时,还应乘以-1;Vsi是回路i中各电动势的代数和。
掌握了通用回路方程的形式和内容,可以很快地直接凭观察写出一个电路的回路方程。
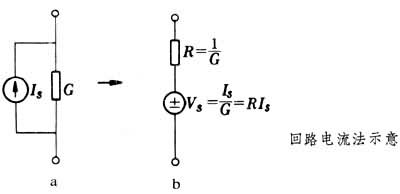
当电路内有如图a所示的支路时,可将其变换成如图b所示的支路,然后再列写方程。
式(1)可简记为
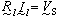 (2)
(2)
式中垾是以自电阻、互电阻为元素的l×l矩阵(l=b-n+1),Il是以回路电流为分量的l维矢量,VS是式(1)的右端项为分量的l维矢量。
对电路进行正弦稳态分析时,用相量法和回路电流法写出的回路方程为
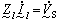 (3)
(3)
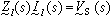 (4)
(4)
回路电流法也会遇到难以处理的支路。这种支路有仅含独立电流源、仅含流控电流源和仅含流控非线性元件的支路。遇到仅含独立电流源的支路可用电源转移的办法(见电路变换)将它移走。遇到后两种支路,最好改用其他方法。
有了回路方程后,便可解方程求出回路电流,再通过回路电流求出支路电流和支路电压。
从数字运算上来看,回路电流法因联立求解的方程数少而优于支路电流法。但此法与节点电压法孰优孰劣则视基本回路数与节点数多少而定。节点数多时本法为优,基本回路数多时则相反,当二者的数目相近时两种方法皆可用。在电路分析的计算机程序中,由于用此法要先寻一组独立回路,就不如节点电压法方便了。