[拼音]:guina luoji
[外文]:inductive logic
逻辑的一个分支。有两个含义:
(1)狭义的归纳逻辑的研究对象是前提和结论之间具有或然联系的归纳推理;
(2)广义的归纳逻辑还包括在进行归纳推理时所使用的科学方法,亦称归纳法。归纳逻辑按其发展的不同阶段,又可以分为古典的归纳逻辑和现代的归纳逻辑两大类型。
古典类型
归纳逻辑的古典类型主要包括枚举归纳法、消去归纳法,同时也包括提出和检验假说的方法。
枚举归纳法从枚举一类事物中的若干分子具有某种性质得出这类事物的所有分子都具有该性质的逻辑方法,就叫枚举归纳法。它的模式是:
S1是 P
S2是 P
…
Si是 P
(S1,S2,…Si不是S类中的全部分子)
所有S是P
枚举归纳法只依靠所枚举的事例的数量,因此,它所得到的结论的可靠程度较低,一旦遇到一个反例,结论就会被推翻。但是,枚举归纳法仍有一定的作用,通过枚举归纳法得到的结论可作为进一步研究的假说。
消去归纳法F.培根所提出的“三表法”和“排斥法”相结合的归纳法,以及J.S.密尔提出的求因果联系的契合法、差异法(见密尔求因果五法),都是消去归纳法。它们的共同特征是:根据所研究的对象有选择地安排事例或实验,然后通过比较消去某些假说,得到比较可靠的结论。以下所说的两种消去归纳法是用条件句的术语对密尔方法的改进。
(1)假定要探求被研究现象 a的必要条件,推广密尔的“求同法”,可以先比较a出现的各种场合。如果发现在 a出现的各种场合的先行情况中仅仅有一个共同情况b,那么b是a的一个必要条件;如果不止有一个共同情况,那么a可能有几个必要条件。显然,在这些场合中的某个场合不出现的情况c不能是a出现的必要条件。如果在先行情况中没有一个共同情况,这并不意味着a没有必要条件。在这里,a的必要条件也许是两个或两个以上先行情况的析取。例如,c和d不是各种场合的共同情况,a出现的必要条件也许是“c或者d”的出现。对“c或者d”还可作进一步的分析。上述方法是密尔的契合法的推广。
(2)假定要探求被研究现象 a的充分条件,根据改进过的密尔的“差异法”,可以选择两种场合,即正面场合和反面场合。在正面场合中,a出现;而在反面场合中,a不出现。反面场合可以选择若干个。然后对几种场合进行比较。如果仅仅有一个先行情况 b属于正面场合但不属于任一反面场合,那么b是a的一个充分条件;如果有两个或两个以上的先行情况属于所有的正面场合但不属于任一反面场合,那么 a可能有几个充分条件。显然,在各个反面场合出现的任一先行情况不能是a的充分条件。如果不存在一个先行情况使得正面场合不同于任一反面场合,这并不意味着 a没有充分条件。因为,a的充分条件也许是两个或两个以上情况的合取。例如,c和d是两种场合中的两个情况,“c并且d”(但不是它们中的单独一个)的出现也许是 a出现的充分条件。上述方法是密尔的“差异法”的推广。
在应用消去归纳法时,充分条件和必要条件可以互相定义。a出现是b出现的必要条件,当且仅当 a不出现是 b不出现的充分条件。例如,施肥是获得丰收的必要条件,不施肥就是得不到丰收的充分条件。在应用消去归纳法确定被研究现象的条件时,利用这种相互关系可以把①、②两种方法结合起来使用。
假说方法假说方法根据一组证据提出一个或一些假说,然后从某一特定的假说演绎出一些结论,这可以写成蕴涵式:"A→B",接着检验这些结论。如果检验的结果是:塡B,根据否定式推理:
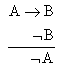
就要否定这个假说。如果检验的结果是B真,就暂时接受这个假说。这里应用的是以下形式的归纳推理:
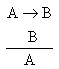
接受或排除一个假说的过程是很复杂的,往往不能一次完成。有时,一个假说可以解释一些现象,但不能解释另一些现象,在这样的情况下,就不能简单地肯定或否定这个假说。一般说来,在两个或两个以上的假说中,能解释的现象数量较大或最大的假说与不能解释的现象数量之差较大或最大的假说,是可以暂时接受的,它们具有较高程度的可靠性。应用假说方法的过程是一个不断地提出、检验、修改、排除或确定假说过程,在这个过程中,需要应用归纳,也需要应用演绎。例如,科学史上关于光的本性的两个著名假说“微粒说”和“波动说”,它们都各自能解释一些光的现象,但又不能完全解释另一些光的现象,只具有一定程度的真实性,后来终于被“波粒二象说”(见波-粒二象性)所取代。
现代类型
19世纪中叶以后,归纳方法的研究和数学里的概率统计相结合,得到了迅速的发展。现代不同的科学领域所应用的归纳方法不尽相同。如在设计科学实验时用培根、密尔的归纳方法与数理统计相结合的方法,在医学和经济学中多应用数理统计。现代归纳逻辑在理论方面的一种发展趋势,就是用数理逻辑的工具对归纳推理进行系统的、形式化的研究,构造出各种归纳逻辑的公理系统。概率逻辑和模态归纳逻辑就是其中的两种。
概率逻辑概率逻辑与数学中的概率统计不同,后者的发展是由于数学和实验科学的需要;而概率逻辑是由于数理逻辑的发展和研究归纳逻辑的需要。概率逻辑从20世纪20年代开始形成不同的系统,在其发展过程中,R.卡尔纳普作出了重要贡献。卡尔纳普把归纳推理主要分为 5种:
(1)直接推理。这是从总体到样本的推理。所谓总体是指所考察的一类事物,样本则是从总体中随机抽出的若干个体组成的子类。直接推理的前提是总体中某一性质M出现的频率,结论是某个样本中M出现的同样频率。
(2)预测的推理。这是从一个样本到另一个不同样本的推理。
(3)类比推理。即根据两个个体之间的相似性从一个个体到另一个个体的推理。
(4)逆推理。这是从一个样本到总体的推理。
(5)普遍的推理。这是从样本到具有普遍形式的假设的推理。
卡尔纳普认为,归纳逻辑是关于归纳推理的理论,是以概率的概念为基础的,归纳逻辑就是概率逻辑。概率是一组命题即某些给定的证据和另一个命题即假设之间的关系,也就是证据对假设的确证度,卡尔纳普称之为概率1,以便与相对频率即概率2相区别。设证据为e,假设为 h,确证度q=c(h,e),c称为确证函数或c函数。卡尔纳普利用数理逻辑和语义学的方法,构造了一个以研究确证度为对象的概率逻辑系统,并对他所提出的 5种归纳推理作了概率的处理。
模态归纳逻辑在概率逻辑发展之后,20世纪中叶以来,有的学者如美国的P.J.科恩用模态逻辑作为处理归纳推理的工具。科恩指出,卡尔纳普的概率逻辑面临不少困难,对归纳推理不宜作概率处理。他所提出的归纳逻辑的研究对象是证据e对假设h的支持度,用s(h,e)表示,s称为支持函数。在他看来,支持度可列为不同的等级,不同等级的支持度,就是证据给予假设不同等级的必然性,一个被证明了的理论就是由较低级的必然性达到较高级的必然性。不同等级的支持度是广义模态逻辑的研究对象。科恩证明了一个广义模态逻辑系统满足他的支持函数的全部要求。
现代归纳逻辑正处在深入研究的新阶段,它与现代形式逻辑即数理逻辑的一些分支,以及与信息论、模糊数学和人工智能等学科密切结合、相互渗透,并以这些学科为工具,不断地开拓新的领域。
- 参考书目
- J.S.Mill,A System of Logic,8th.ed.,London,1872.
- R.Carnap, Logical Foundations of Proda dility,Chicago,1950.
- L.J.Cohen,The Implications of Induction,London,1970.