[拼音]：xiangguan hanshu
[外文]：correlation function
描述系统的物理量在空间两点或两个时刻涨落的相互关联的函数。前者称为空间相关函数，后者称为时间相关函数。
空间相关函数
描述外界在空间某点的扰动对空间另一点的影响，给出原因同结果在空间上的联系。在平衡态的系统中，由于粒子间有相互作用，不同粒子的相对位置之间就一定存在相关性。定义物理量A(r)在两个不同位置r，r┡上的涨落ΔA的相关函数为
，
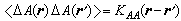式中< >表示系综的平均值，可以把它看作是位置的连续函数，而ΔA(r)＝A(r)－<A(r)>。A(r)可以是能量密度E(r)、粒子数密度n(r)，也可以是磁矩密度（或磁化强度）在z方向的投影Mz(r)，电偶极矩密度P(r)等。
相关函数 K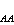
是描述空间两处涨落的相互联系程度的量。如果r，r┡两处的涨落是相互独立的，则
。
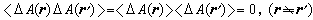若系统是均匀的，相关函数就是两点位矢差 r－r┡的函数，相关函数的值应随两点间距离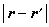
的增大而减小。当距离无限增大时，相关性一定消失。如果在距离
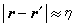内，相关函数随
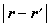变化很大，相关性显著，但在η以外，相关性很弱甚至可以略去，则可用η作为空间相关性范围的一种量度并称 η为关联长度。若物理量在空间任何两点都不相关，就相当于关联长度为零的情形。这时相关函数应为
。
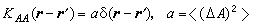物理量在空间两处涨落的关联，来自系统内部粒子间的相关性，这种相关性可分为两类：一类是由于粒子间存在相互作用，使得空间各处相互牵连，叫做动力学相关性；另一类是由于微观粒子的全同性而产生的量子效应，叫做统计相关性（对于独立粒子系统，量子统计规律表明，费密粒子系统具有排斥相关性，玻色粒子系统具有吸引相关性）。但这两类相关性之间往往是相互联系、相互影响的，不能把它们截然分开。
空间相关函数是一个重要的量，利用它可以求出系统的诸热力学量。
无外场存在时的均匀系粒子数密度在 r处的值为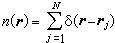
。此式说明当粒子j的位置rj进入r 处的一个无限小体元中时，对r处粒子数密度的贡献为1，而各个粒子同时分别出现在r1、r2、…rN处附近的几率为 
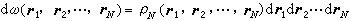，其中
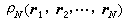代表位置的几率密度函数。若定义二粒子几率密度函数
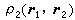为
，
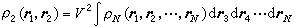式中 V为系统的体积。则可以求得粒子数密度涨落的空间函数为
，
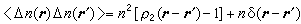式中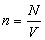
是粒子数密度，为一常数。对于均匀系统，
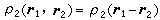，表示不管其他所有粒子的位置如何，两个粒子同时分别处于r1和r2的几率密度。如果粒子是相互独立的，这几率密度应等于
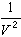，因而有ρ2(r1，r2)=1， 如果
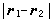很大，则有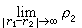
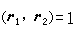，即r1和r2两点是独立的。若知道了ρ2，就不难求出系统的各个热力学量。
由于外场如磁场、化学势场等的引入，使系统不均匀，并使得系统有一附加的能量。若改变外场，会引起系统的能量或粒子数密度以及几率分布函数发生相应的变化，也会引起平均磁化密度、平均能量密度或平均粒子数密度等的变化，从而可以导出联系各种量的涨落相关函数和一些热力学量的导数的关系式。
例如，当磁场Hr(r)变为Hr(r)+δHr(r)时，磁化密度平均值的变化为
，
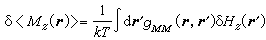能量密度平均值的变化为
，
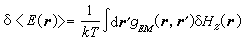如果只在r1处的磁场有一变化，那么有
，
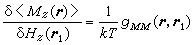可见，相关函数ɡ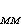
(r，r1)描述了由于r1处磁场发生变化，而使r 处磁化密度受到影响的强弱以及这种影响在空间的范围。
同样可以有
，
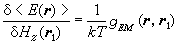ɡ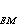
(r， r1)的物理意义是表征r1处的磁场变化对r处能量密度的影响，称为能量密度－磁化密度混合相关函数。
若外场的改变量同位置无关，是一常量，即δHz(r)＝δHz，那么容易得到磁化率的表式为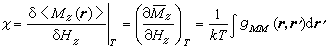 
，同样有
，
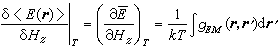上两式中的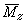
和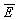
都是热力学量，分别为单位体积的磁矩和内能。这两个式子把各种量的涨落相关函数和一些热力学量的导数联系起来了。
以上讨论也同样适用于空间某处有“化学势场”或“温度场”变化的情形，并可得到类似的结果。
临界点附近在此区域，物质系统中各物理量的空间相关性比通常条件下要强得多。通过在居里温度（见铁磁性）附近、弱磁场情况下对铁磁体的研究发现，距离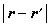
小的时候，相关函数ɡ
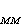按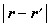
-1的规律变化，在η的范围以内，相关性都是显著的；当距离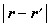＞η以后，ɡ
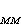按指数规律衰减。因此，称η为磁相关长度。当T→嘷 (居里温度)时，η→∞，这时，相关函数按
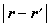-1的规律变化，相关性随着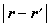的增大衰减很慢，而且在相当大的范围内都是如此。于是得出结论，在临界点附近，相关性变得很强，相关性是长程的。
经典理想气体中粒子的位置间没有相关性，但在量子理想气体中，尽管粒子间没有相互作用，但由于粒子全同性导致的量子效应，使粒子以间接方式彼此发生“相互作用”，从而具有相关性。运用二次量子化方法，可以求出量子气体的相关函数为
。
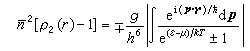式中上面的符号对应费密子系统，下面的符号对应玻色子系统。并可以求得密度涨落的傅里叶分量均方值的公式
。
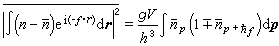式中ɡ=2s+1为自旋简并度，ε、μ分别为单粒子能级和化学势，V是系统的体积，嬞p是与动量p对应的单粒子态的平均粒子数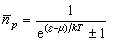 
，式中“+”号对应费密分布，“－”号对应玻色分布。由相关函数公式可知，对于费密气体嬞2[ρ2(r)-1]＜0，即空间一点某粒子的存在，使得另一粒子出现在这点附近的几率减小；对于玻色气体嬞2[ρ2(r)-1]＞0，即空间一点某粒子的存在，使得另一个粒子出现在这点附近的几率增加。前者表明粒子间存在着排斥相关性，后者表明粒子间存在着吸引相关性。当h→0时，就过渡到经典力学极限情况，此时由于相关函数公式右边被积函数中因子
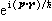的波矢或相应地频率无限地增加，因而积分趋于零，所以相关函数变为零，这正是预期的经典理想气体的结果。
时间相关函数
描述某一时刻的扰动对另一时刻物理量的影响，给出原因和结果在时间上的联系。引进时间相关函数的一个典型途径就是布朗运动。
布朗运动布朗粒子是直径为10-5～10-7米的微小粒子，它受到周围媒质分子的不平衡的碰撞作用，其中一部分是宏观的粘滞阻力，它具有平均的效果。当粒子的速度v不大时，粘滞阻力为－αυ；另一部分是涨落力。粒子在合力作用下，作无规则的运动，它的运动方向和速度变化极快。由于这种涨落力是随机力，所以经过很短的时间Δt（比媒质分子与布朗粒子碰撞时间长得多）以后，粒子加速度的大小和方向都同Δt之前没有关联。因此，可以用时间相关函数描述这种随机变量在时间上的相关性。
以A(t)代表布朗粒子在涨落力作用下得到的加速度，则定义它的时间相关函数为
，
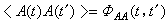式中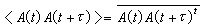
=
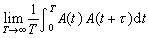
是在时间间隔τ给定时，对t长时间的平均。显然，如果τ足够长，A(t)和A(t+τ)已不相关。这就是说，在不同时刻t，A(t)和A(t+τ)所取的数值和符号都是相互独立的，以致A(t)和A(t+τ)的乘积取各种可能的数值以及取两种符号的几率相等，于是上式等于零，因而相关函数也等于零。如果给出τ的数值是在某一范围时，平均值不等于零，那么A(t)和A(t+τ)是相互关联的。若τ的数值极小，从宏观上趋于零，则A(t)和A(t+τ)不存在关联，可以把时间相关函数写成
，
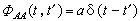其意义是:t厵t┡时，相关函数等于零；t=t┡时，相关函数等于A2(t)>，由于A=0，所以A2 (t)>是A(t)的均方涨落， a是描述随机变量A(t)的涨落大小的量。A的涨落越大，a就越大。由于布朗粒子受到的涨落力也属于这种类型，所以它的相关函数也满足上式。
若把每个布朗粒子当作一个同周围媒质处于热平衡的系统，则每个系统的长时间平均值应等于同一时刻的系综平均值。A(t)和A(t＋τ)的乘积可以看作是布朗粒子的一种物性。这样，时间相关函数又可写作
，
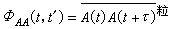式中右端表示同一时刻t对所有布朗粒子的平均。
在平均力和涨落力的作用下，布朗粒子的运动遵从朗之万方程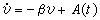 
。即布朗粒子速度随时间的变化是两部分力联合作用的结果，这种作用是积分效应。由于平均力相对涨落力是相关的，所以速度也是相关的。因此，虽然速度同涨落力都是随机变量，但它们的行为却不同。
考虑布朗粒子一维运动的情况：在初始时刻t0，以某个确定的速度注入一束布朗粒子。通过对朗之万方程求解，得到υ(t)的表示式，再对所有布朗粒子求平均，并注意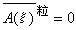到
，即可得到
。
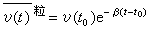可见，布朗粒子的平均速度随时间呈指数衰减，其弛豫时间为 τ0＝β-1。若以15℃的水作媒质，设粒子为半径3.67×10-5cm的圆球，则可算出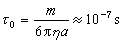
。即经过 10-7s，平均速度已经很小。 这样，最后可以得到
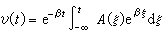，从而求得速度的相关函数为
。
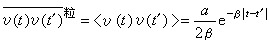此式表明，速度具有相关性，其相关函数包含两个因子，一个是同涨落力的均方涨落有关的关联强度，另一个是随时间衰减的因子。关联时间是 τ0＝β-1，它决定于媒质的粘阻，这种粘阻是一种耗散机制，而作为平均力的量度β，正是它的强度。同时，容易算出布朗粒子的均方位移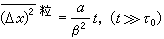
。而速度的均方值应是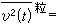
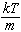。再利用速度相关函数公式，可定出
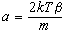。由此可见，系统的耗散愈强，则涨落力的涨落就愈大。这个结论反映了涨落耗散定理的内容。
可以把关于布朗粒子速度时间相关性的讨论，推广到系统的任何一个随机变化的物理量A(t)。当系统处于统计平衡时，A(t)是广义坐标和广义动量的函数，由于对系综的平均和固定τ对t长时间的平均结果相同，于是可将A(t)在两个不同时刻的相关函数定义为
。
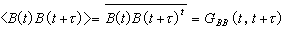统计平衡系统中，任一随机变化物理量的时间相关函数具有如下一些性质：
（1）相关函数只是时间间隔的函数，即
G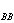
(t，t+τ)＝G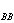(τ)。
这是因为平衡态不随时间变化，两个不同时刻的物理量之间的相关性，应同观察时间无关。
（2）若时间间隔远大于关联时间，那么，它们之间的关联消失，因而
A(t)A(t+τ)＝A(t)A(t+τ)。只要A等于零，相关函数G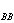就等于零。关联时间和关联强度决定于系统本身的动力学性质。
（3）相关函数G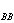(τ)是时间τ的偶函数，即有
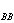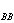G(τ)＝G(-τ)。
这是因为A(t)对以后时刻的影响和它对以前时刻A(t-τ)的依赖性在强度上应该一样。
（4）对于不同物理量在时间上的关联，可以由公式A(t)A(t┡)>=G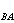
(|t't|)定义的交叉相关函数来描述。例如B(t)代表在t时刻外界的扰动，A(t)是系统的某个随机变化的物理量，则上式中的G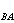(|t't|)就是描述外界扰动对系统某个物理量的影响在时间上的关联。
采用傅里叶分析，把某个随机变量按不同频率进行分解，从而可以了解不同频段对相关性的贡献。将随机变量A(t)及其时间相关函数G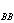
(τ)展开成傅氏积分，运算后可得到一个重要的关系
ɡ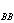(w)＝<|b(w)|2>，
式中w是频率，b(w)和g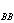(w)分别是A(t)和G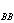(τ)的傅氏系数或谱密度。还可以得到联系随机变量的二次方涨落和相关函数的傅氏分量的表示式
，
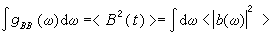例如，对于布朗粒子的运动，就有
，
，
。
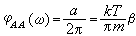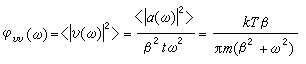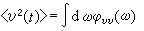以上各式中v(ω)和ɑ(ω)分别是布朗粒子的速度和涨落力的傅氏系数，而嗞
(ω)和嗞
(ω)分别是速度和涨落力相关函数的谱密度。这些关系也可用于电路中的涨落现象。
L.昂萨格假定，在线性区近平衡的非平衡态，相当于一个偏离平衡的涨落，非平衡系统随时间的变化和平衡系统中涨落的变化遵从相同的规律。在这个假定下，运用时间相关函数在时间平移变换t→t-τ 和变换 τ→-τ（即微观可逆性）下的不变性，可以证明不可逆过程热力学中的昂萨格倒易关系。