[拼音]:dianzhen donglixue
[外文]:lattice dynamics
研究晶体中的原子在平衡位置附近的振动和这些振动对晶体性质的影响的学科。它是固体物理的基础之一。
历史
点阵动力学的研究始于20世纪初。1907年,A.爱因斯坦发表了题为“普朗克辐射理论与比热的理论”的论文,他把N个原子组成的晶体,看作是3N个相互独立的具有同一频率的谐振子;并认为这些振子的能量也应按普朗克的理论量子化,从而说明在温度趋于绝对零度时,晶体中由原子运动贡献的比热趋向于零这一实验事实。爱因斯坦的工作不仅是点阵动力学的开始,而且在量子理论的发展上也起了重要作用。但他所得到的热容公式在低温下接近于零的趋向显得比实验结果快(见爱因斯坦模型)。P.J.W.德拜在1912年认识到,爱因斯坦热容公式与实验不大符合的原因在于没有考虑到晶体中原子振动频率并不是完全相同的。德拜把晶体当成连续媒质来求得振子频率分布,得到了更符合实验结果的比热容公式,德拜的理论能比较简明地概括实验材料,在推动点阵动力学的发展上,起过较大作用(见德拜模型)。同年,M.玻恩和T.von卡门发表了题为“论空间点阵的振动”的论文,提出晶体中的原子振动应以点阵波的形式存在。他们的论文包含了现代点阵动力学的大部分基本概念和原则,是点阵动力学的奠基性著作。从20年代到40年代,人们进一步完善了点阵动力学的基本理论;点阵振动对晶体的热力学性质、热传导、电导、介电和光学性质、X射线衍射等方面的理论和实验研究也发展了起来。这些都比较完全地总结在玻恩和黄昆的专著《晶体点阵的动力理论》一书中。50年代以来,点阵动力学在实验研究上有了很大的进步,特别是利用中子非弹性散射直接测定点阵振动的色散关系(见点阵动力学的实验研究方法)。
研究内容
点阵动力学主要研究以下几个方面。
基本概念如果不考虑晶体边界的影响,可以认为讨论的是一个无限的晶体点阵。设每个元胞中有 s个原子,元胞L中第k个原子的位置记作 ,它的平衡位置记作
,它的平衡位置记作 ,r(L是元胞L的位置的点阵矢,r(k)是第k个原子在元胞L中的相对位置。 原子对平衡位置的偏离记作
,r(L是元胞L的位置的点阵矢,r(k)是第k个原子在元胞L中的相对位置。 原子对平衡位置的偏离记作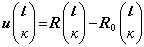 。在绝热近似下,可以认为晶体原子相互作用的势能仅是原子的位置的函数,原子的平衡位置是它的极小值。把势能函数展开为对平衡位置的偏离的级数,显然,一次项应为零;如果只考虑到二次项,便得到势能函数嗞的二次近似展开式
。在绝热近似下,可以认为晶体原子相互作用的势能仅是原子的位置的函数,原子的平衡位置是它的极小值。把势能函数展开为对平衡位置的偏离的级数,显然,一次项应为零;如果只考虑到二次项,便得到势能函数嗞的二次近似展开式
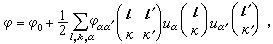 (1)
(1)
式中 是
是 的三个分量。
的三个分量。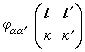 称为力常数,这个近似称为简谐近似。显然,它应该只依赖于L-L┡,而不是分别依赖于L和L┡。从式(1)可得到点阵中原子的运动方程
称为力常数,这个近似称为简谐近似。显然,它应该只依赖于L-L┡,而不是分别依赖于L和L┡。从式(1)可得到点阵中原子的运动方程
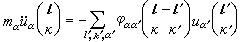 , (2)
, (2)
式中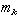 是第k个原子的质量。这是一个无穷维的周期性的方程。显然,它有下列波动形式的解
是第k个原子的质量。这是一个无穷维的周期性的方程。显然,它有下列波动形式的解
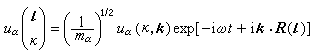 ; (3)
; (3)
式中k是波矢,因此uα(k,k)满足的方程是
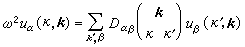 。 (4)
。 (4)
这是一组3s维的方程。其中系数是
 , (5)
, (5)
 称动力矩阵。式 (4)有解的条件是系数行列式为零:
称动力矩阵。式 (4)有解的条件是系数行列式为零:
 , (6)
, (6)
式中δ是克罗内克符号,即当 α=β时,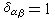 ;反之
;反之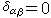 。因此,给定一个波矢k,从式(6)可得到3s个频率ω=ωj(k),(j=1,…,3s),把每个频率代入式(4)得到一支点阵波:
。因此,给定一个波矢k,从式(6)可得到3s个频率ω=ωj(k),(j=1,…,3s),把每个频率代入式(4)得到一支点阵波:
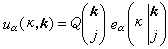 , (7)
, (7)
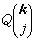 是指这支波矢为k,频率为 ωj的点阵波的振幅。
是指这支波矢为k,频率为 ωj的点阵波的振幅。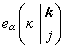 是一个归一化的3s维的矢量
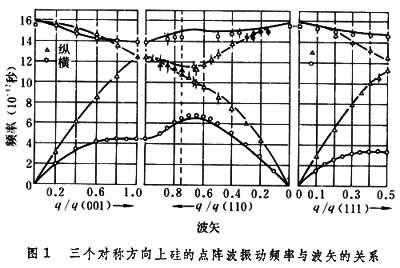
是一个归一化的3s维的矢量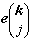 的分量,它表示振动的方向。这样得到的3s支点阵波中,其中有三支是与把晶体看作连续媒质时的三支弹性波相对应,它们的频率ωj(k)在k趋于零时应趋于零。这三支称声频支或点阵波的声频模。另外的3s-3支称光频支或点阵波的光频模。k→0时的光频支反映了元胞中原子的相对振动。图1是三个对称方向上硅的点阵波振动频率与波矢的关系。
的分量,它表示振动的方向。这样得到的3s支点阵波中,其中有三支是与把晶体看作连续媒质时的三支弹性波相对应,它们的频率ωj(k)在k趋于零时应趋于零。这三支称声频支或点阵波的声频模。另外的3s-3支称光频支或点阵波的光频模。k→0时的光频支反映了元胞中原子的相对振动。图1是三个对称方向上硅的点阵波振动频率与波矢的关系。
两个波矢相差一个倒易点阵矢量的点阵波是等效的,因此可把点阵波的波矢 k的取值范围限于波矢空间的特定的多面体,它称为第一布里渊区。k的允许值取决于对解所加的边界条件。很显然,对足够大的晶体来说,选择不同的边界条件对从解所得到的晶体的“体”的性质是不会有影响的。H.韦耳(1911)、W.莱德曼(1944)对此给出过严格的数学证明。通常,都采用玻恩和T.von卡门的做法,想像把晶体取成为每边有L个元胞的立方体,要求该立方体相对的面上的解相等。这个边界条件限制了波矢k的取值为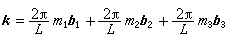 ,m1、m2和m3是整数b1、B2和B3是点阵的倒易点阵的基矢。显然,在第一布里渊区中k的取值可以有L3个,即这个立方体所包含的元胞数。每个k有3s个点阵波,因此共有 3sN(N=L3)个点阵波。晶体中任一个原子的运动可以用这3sN个点阵波的叠加来表达。注意到这个立方体中包含有sN个原子,有3sN个运动自由度;所以用点阵波来表达可以看作是对这个振动系统的一个坐标变换,从这个观点,就很容易把点阵动力学的理论发展成为量子理论。
,m1、m2和m3是整数b1、B2和B3是点阵的倒易点阵的基矢。显然,在第一布里渊区中k的取值可以有L3个,即这个立方体所包含的元胞数。每个k有3s个点阵波,因此共有 3sN(N=L3)个点阵波。晶体中任一个原子的运动可以用这3sN个点阵波的叠加来表达。注意到这个立方体中包含有sN个原子,有3sN个运动自由度;所以用点阵波来表达可以看作是对这个振动系统的一个坐标变换,从这个观点,就很容易把点阵动力学的理论发展成为量子理论。
在简谐近似下,这个晶体的哈密顿量是

如选择另一组简正坐标,作以下的坐标变换:
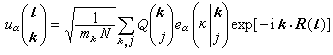 (9)
(9)
代入式(8),考虑到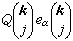 的定义和满足的条件,就能得到
的定义和满足的条件,就能得到
 。 (10)
。 (10)
这是 3Ns个相互独立的谐振子组成的系统的哈密顿量。振子有频率分布ωj(k)。因此,通常说点阵波是点阵振动的简正模。当然,简正模可有几种不同的但是是等效的选法。这里选的是行波式的简正模,在上述坐标变换的基础上,如果把简正坐标 及
及 当成量子力学的力学量,不难建立起点阵动力学的量子力学形式。
当成量子力学的力学量,不难建立起点阵动力学的量子力学形式。
有了ωj(k),就可求得在简谐近似下点阵的热力学函数。例如内能 和定容热容Dv就是
和定容热容Dv就是
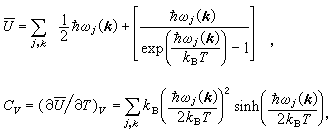 (11)
(11)
式中kB是玻耳兹曼常数。可以引入点阵振动频谱来进行这些计算。频谱 g(ω)的定义是在频率ω附近单位频率区间中的点阵波模的数目。因此,式(11)可写为
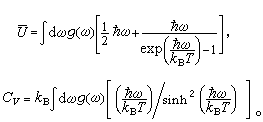
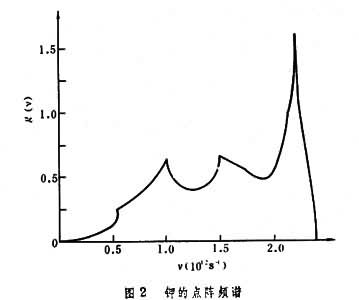
由已知的ωj(k)来求g(ω)是一个数学问题。图2是从中子非弹性散射实验测得的钾的ω(k)计算得到的频谱g(ω)。图上看到g(ω)并不是很平滑的函数。其实频谱上经常会有一些奇异性,这是各类元激发的谱常有的一种现象。
德拜模型相当于假定了一种特别简单的频谱形式
 (12)
(12)
B由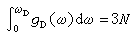 来决定。因此,德拜谱只有一个参数ωD。把gD(ω)代入Dv的表达式,在T比较低时,可得到点阵定容热容的T3规律
来决定。因此,德拜谱只有一个参数ωD。把gD(ω)代入Dv的表达式,在T比较低时,可得到点阵定容热容的T3规律
 ,
,
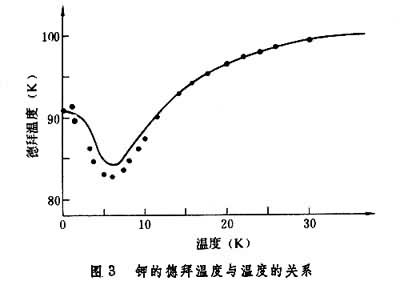
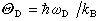 称德拜温度。嘷D作为材料点阵振动频率的一个粗略估计,有一定参考意义。但如果真正用德拜模型的热容公式来处理实验测得的比较精确的热容数据,就会发现得到的嘷D乃是温度的函数,考虑到德拜的频谱与实际频谱的差异很大,这是很自然的。图3给出的是这样处理钾得到的结果,所以,必须注意德拜模型的适用性。
称德拜温度。嘷D作为材料点阵振动频率的一个粗略估计,有一定参考意义。但如果真正用德拜模型的热容公式来处理实验测得的比较精确的热容数据,就会发现得到的嘷D乃是温度的函数,考虑到德拜的频谱与实际频谱的差异很大,这是很自然的。图3给出的是这样处理钾得到的结果,所以,必须注意德拜模型的适用性。
但只基于简谐近似来计算晶体的热力学性质仍是不够的(见非谐相互作用)。
极性振动与晶体的介电性质和光学性质离子晶体中,正负离子的相对位移会产生电偶极矩。长波的光频模相应于元胞中原子的相对移动,可以按它是否产生电偶矩来把它区分为极性振动和非极性振动两类。极性振动必定伴随着宏观的电磁场。因此,必须同时考虑点阵运动的方程和电磁场的方程。黄昆(1951)最先对立方晶体元胞中有两个离子的情况作了系统的处理。这时,应有三个光频支:一个纵波和两支横波,都是极性振动。纵波与横波有一个显著不同,纵波会产生束缚电荷,出现宏观的库仑场,所以长波的纵光频支比横光频支有较高的频率。可以证明,在这种情况,波矢趋于零的纵光频支频率 与横光频支频率
与横光频支频率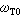 之间有下列关系
之间有下列关系
 , (13)
, (13)
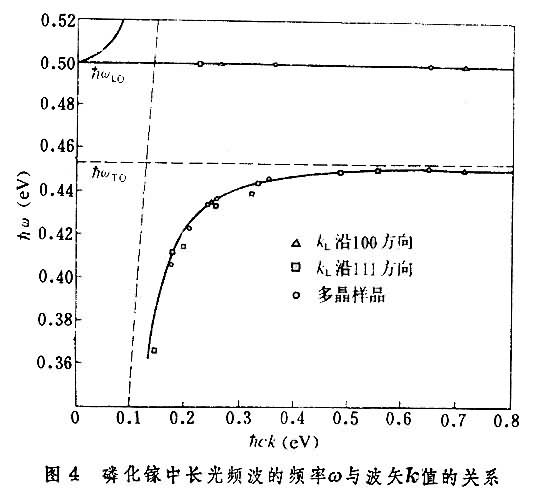
ε(0)是晶体的静电介电常数。ε(∞)是频率远高于点阵振动频率时的介电常数。这关系称为 LST关系。横波则能与外来的电磁波耦合,对点阵的介电性质有贡献。电磁波和横向极性振动的耦合产生了新的耦合模式,它是电磁波与点阵波的耦合模,称为极化激元。这是黄昆所首先引入的概念。图4是实验上测量得到的磷化镓中点阵振动的色散关系。虚线是不考虑这个耦合时的色散关系,实线是耦合模式的色散关系。
 点阵振动的色散关系与力模型
点阵振动的色散关系与力模型
50年代以来,有了准确测定整个布里渊区中点阵波的色散关系 ωj(k)的方法(见点阵动力学的实验研究方法),由此提供了定量地检验这些理论的可能性。除了求解的数学技巧外,这中间最主要的是关于点阵原子间的相互作用的力模型。
最易想到的是所谓“刚性离子”模型,把晶体势看作是各对原子之间的势能之和,并认为它只决定于这个原子之间的距离:
 。 (14)
。 (14)
对微小位移偏离作展开,每对原子之间便有两个力常数──径向的和切向的。经验证明,对固态惰性元素和简单金属来说,适当选择力常数,刚性离子模型能给出与某些实验相当符合的结果。从严格的刚性离子模型出发,可导出弹性常数应满足柯西关系;但对多数金属(包括碱金属)来说,柯西关系都符合得相当不好。所以需要对这问题作进一步研究。
对离子晶体和价键晶体,经验证明,壳层模型更合适一些。它把每个原子(离子)看作是由一刚性的“实”和一带电的“壳”组成,实和壳之间近似地由一各向同性的力常数表征其联系;同一原子的实和壳之间也可相对移动;不同原子之间的相互作用则包括各自的实和壳相互之间的各种组合。壳层模型是一个唯象的模型。从能带论和多体理论的观点也提供了它的适用性的一定理论基础。
相变和点阵振动F.林德曼(1910)曾提出,固体的熔化发生在点阵振动的平均振幅与原子之间的距离可以比拟的情况下。实验数据表明这个观念有一定的合理性,同一类固体的这个比例还常常是差不多的。但一个严格的关于熔化与点阵振动之间的关系的理论还没有建立起来。在结构相变(见固体中的相变)中,点阵振动起着关键的作用。
- 参考书目
- M. Born and T.von Karman, Physik Z.,J.-Nr.13,S. 297,1912. M.Born and K.Huang, Dynamical Theory of CrystalLαttices,Oxford Univ.Press, London and New York, 1954.