[拼音]：hanshu
[外文]：function
数学的基础概念之一。在物质世界里常常是一些量依赖于另一些量，即一些量的值随另一些量的值确定而确定。函数就是这类依赖关系的一种数学概括。
设D是一非空的实数集，ƒ是某一规则。如果对每一个数x∈D，ƒ 惟一地确定出一个相对应的实数ƒ(x)，则称ƒ为定义于D上的一个函数，集D 称为函数的定义域。数ƒ(x)称为函数在x的函数值，全体函数值的集M={ƒ(x)|x∈D}=ƒ(D)称为函数的值域。一般，由规则ƒ在D上定义的函数用记号
ƒ:D→M
表示，也常常简单地记作ƒ。函数ƒ:D→M是从集D到集M上的映射。
函数定义域D的一些最简单情形可以是整个数轴，即全体实数的集R；也可以是数轴上的某个闭区间[α，b]={x|α≤x≤b}或开区间(α，b)={x|α<x<b}。规则ƒ通常用某种计算公式表示，或用图表文字加以说明。所谓一个函数已知，就是说确定这函数的要素（定义域和对应规则）是给定的，从而值域也是给定的。
函数记号ƒ:D→M准确地表现了函数概念的内涵。但是人们需要能简便表示函数的其他方法。目前科学著作中比较流行的做法是允许把函数ƒ:D→M记作ƒ(x)(x∈D)或者更简单地记作ƒ(x)（如果定义域 D是不写自明的）。例如：对一切实数x，规则 ƒ(x)=2x3-1将定义出一个函数ƒ:R→R，通常人们就把它记作2x3-1(x∈R)或者 2x3-1。严格说来，这样做是有缺陷的，因为它多少混淆了函数ƒ与数（函数值）ƒ(x)。不过它仍然被广泛采用。
设给定任一函数 ƒ:D→M。如果令x是一个以D为变域的变量（不再像前面那样表示D中的某一个数），令y是一个以M为变域的变量，那么，函数ƒ显示的是：对于变量x在D内所取的每一个值，通过ƒ能给变量y在M内惟一地确定出一个对应值。由此可见，变量y通过ƒ表现出对变量x的一种依赖关系，而函数ƒ则是这种依赖关系的数学表达。
在给函数概念添加上变量这一层含义的时候，总把以函数定义域D为变域的变量叫做函数的自变量，把以函数值域M为变域的变量叫做函数的因变量。于是在上面的作法中，x是自变量，y是因变量。“变量y通过函数ƒ依赖于x”这个事实也常常被简单地说成“变量y是变量x的ƒ函数”，并且用y=ƒ(x)这种等式形式的记号来加以表示。
把函数理解成变量间的依赖关系，丰富了人们对这个抽象数学概念的直觉联想。但这并不丝毫改变函数的本质内容。特别说来，用什么名称来称呼一个函数的变量是无关紧要的。记号y=ƒ(x) (x∈D)和s=ƒ(t)(t∈D)在数学上表示的是同一个函数ƒ:D→M。
函数的图像
对任意一个函数y=ƒ(x)(x∈D)，如果把D中的任意一个数x与它的对应数y(=ƒ(x))组成一个有序数对(x，y)，相应地便在坐标平面xOy上得到一点P(x，y)。平面上所有这种点（数对）的集
G ={(x，y)|x∈D，y=ƒ(x)}
称为函数ƒ的图像（图1
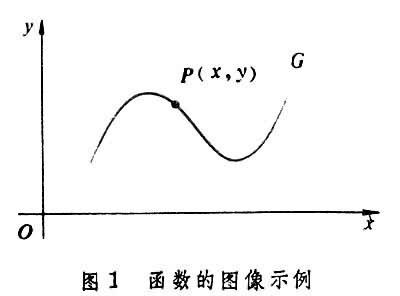
）。由函数定义，集G具有下述性质：若(α，b)，(α，с)都属于G，则b=с，就是说，G不含有第一个坐标（第一个数）相同但相异的点（数对）。从这一性质出发，如果给定了集G，那么函数本身（定义域和对应规则）也就随之完全确定。所以，每一个函数都可以定义为某一个具有上述性质的点（有序数对）之集。
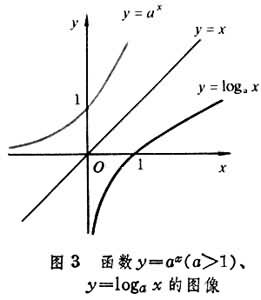
一切所谓的基本初等函数，包括常值函数y=с(常数)，幂函数y=xα，指数函数y=αx，对数函数y=logαx，三角函数y=sin x，…，反三角函数 y=arc sinx，…等等的图像，都可以用通常的绘图工具比较满意地画出，它们各形成平面上的一条或者多条曲线（图2、图3、图4、图5）。
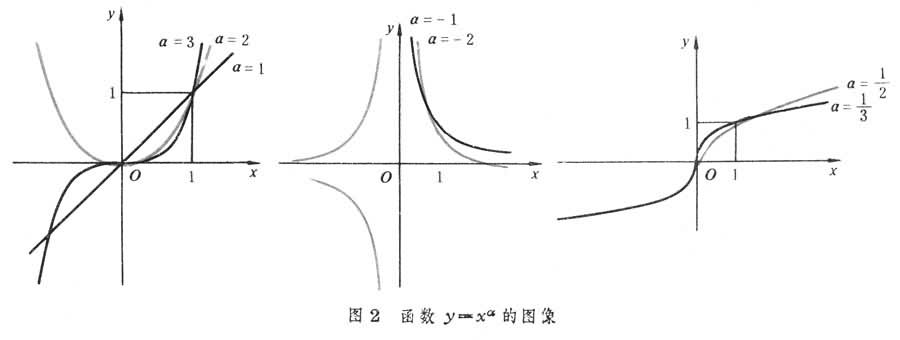
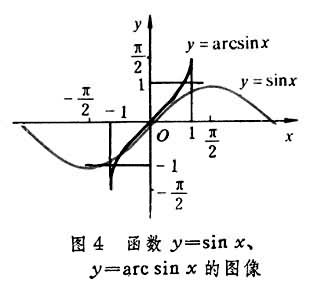
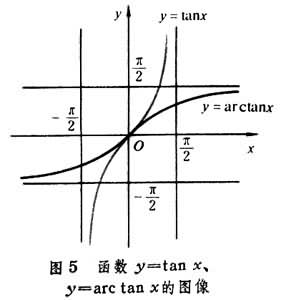
不过不是对所有的函数都能做到这一点，定义于[0，1]上的狄利克雷函数“D(x)=1，当x为有理数时；D(x)=0，当x为无理数时”就是一例。
常见的函数
常值函数是一种很特殊的函数。除了它以外，下列几种函数ƒ:D→M也各具特点，而且常常被用到。
（1）恒等函数 如果对D中一切x有ƒ(x)=x，则称ƒ为D上的恒等函数，有时使用专门的记号I表示。
（2）有界函数 如果存在常数A（常数B），使得对D中一切x有A≤ƒ(x)(ƒ(x)≤B)，则称ƒ在D上有下界（有上界），数A（数B）为ƒ的一个下界（上界）。如果ƒ在D上既有下界又有上界，则称ƒ 为D上的有界函数。
（3）单调函数 如果对D中任意两数x1，x2，当x1<x2时，都有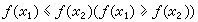
，则称 ƒ为D上的增函数（减函数）。如果对上面所说的x1，x2，严格不等式
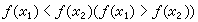总成立，则称ƒ为D上的严格增函数（严格减函数），增函数与减函数统称为单调函数；严格增函数与严格减函数统称为严格单调函数。
（4）奇函数和偶函数 如果D是关于原点对称的数集，即当x∈D 时必有-x∈D，且对D 中一切 x等式 ƒ(-x)=-ƒ(x)(ƒ(-x)=ƒ(x))总成立，则称ƒ为D上的奇函数（偶函数）。
（5）周期函数 如果存在常数T≠0，使得对D中一切x，等式ƒ(x+T)=ƒ(x)总成立，则称ƒ为D上的周期函数，T为ƒ的一个周期。每一周期函数实际上都有无穷多个不同的周期。如果在它们之中存在一个最小的正周期TD，则称TD为函数的基本周期。
（6）数列 如果D为全体自然数的集，则称ƒ为一个数列。通常把这种函数的函数值用同一字母(例如 α)附加体现自变量的值的下标的办法加以表示：
ƒ(1)=α1，ƒ(2)=α2，…，ƒ(n)=αn，…。
称α1为数列的第一项，α2为第二项等等，αn为通项。数列本身则通常写作
α1，α2，…，αn，…，或简记作{αn}。
函数的运算
在函数与函数之间还常常进行一些运算。设有函数ƒ(x) (x∈A)及g(x) (x∈B)，倘若集D =A∩B不是空集，那么通过等式
(ƒ+g)(x)=ƒ(x)+ g(x) (x∈D)，
(ƒ-g)(x)=ƒ(x)- g(x) (x∈D)，
(ƒ·g)(x)=ƒ(x)·g(x) (x∈D)，
在集D上定义出新的函数ƒ+g，ƒ-g，ƒ·g，分别叫做函数ƒ与g的和（函数）、差、积。如果集E＝A∩{x|x∈B，g(x)≠0}不是空集，则由等式
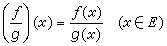
在集E上定义出一个新的函数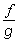
，称为函数ƒ除以函数g的商。
除四则运算外，函数间的下一个运算也是十分重要的。设集F={x|x∈B，g(x∈A}不是空集，那么通过等式
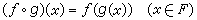
在集F上所定义出的新的函数 ƒ。g，称为函数ƒ与函数g的复合函数。一般说来，复合函数ƒ。g和g。ƒ是不同的函数。
类似地可以考虑多个（两个以上）函数的四则运算和相继复合的运算。基本初等函数经有限次四则运算和复合运算所得到的一切函数统称为初等函数。
对于函数ƒ:D→M或者y=ƒ(x)(x∈D，ƒ(D)=M)，如果当x1，x2为D内两个不同数时必有ƒ(x1)≠ƒ(x2)，那就出现下述的情况：对于集M中的每一个数y，集D中有且仅有一个数x使得ƒ(x)=y。如果就让这个数x与y相对应，便立刻得到一个定义于集M上的新函数，称为ƒ的反函数，记作
ƒ_1:M→D 或 x=ƒ_1(y)(y∈M)。
如果函数ƒ有反函数，那么ƒ在集D和M的元素之间就建立起一一对应关系，所以ƒ也是ƒ_1的反函数。习惯上常常把函数y=ƒ(x)的反函数x=ƒ-1(y)改写为y=ƒ-1(x)(x∈M)。后者的图像如果同函数y=ƒ(x)的图像画在同一坐标平面上，它们关于直线y=x是对称的（图3）。
由反函数定义，下面两个等式恒成立：
y-ƒ(ƒ-1(y))=0 (y∈M)，x-ƒ-1(ƒ(x)=0 (x∈D)。
由此，例如从前一等式出发，可以把函数x=ƒ-1(y)看作由方程y-ƒ(x)=0确定的隐函数。
函数概念的推广
以上谈到的都是只含一个自变量的函数，并且集D和M都限定为实数集，即所谓的“一元(实)函数”。然而在数学及其应用中，考虑多元（n 元，n≥2）函数是必要的。不仅如此，数学科学的近代发展还一再导致了函数概念的其他推广:集D和M从实数集推广到复数集，进而更推广到任意两个集的情形。例如，如果让平面上每一个圆x对应到它的面积y，那么y将是x的函数。在这里 x就不再是数而是几何图形。如果让空间的每一个球x对应到它的中心y，则y也将是x的函数。这时，x与y都已不再是数了。
函数的一般定义可以陈述如下。设D={x}，Y={y}为两个任意的非空集，而ƒ为满足下述条件的有序对(x，y)的集:x∈D，y∈Y，且对于每一元素x∈D， 恰有一元素y∈Y使得(x，y∈ƒ，这时便称ƒ为定义于D上的一个函数，记作ƒ:D→Y或ƒ，有时也记作y=ƒ(x)(x∈D)或ƒ(x)(x∈D)。集D称为函数ƒ的定义域。对于任一元素x0∈D，由函数定义恰有一元素y0∈Y使得x0，y0)∈ƒ，人们称这个元素y0为函数ƒ在x0的函数值，记作ƒ(x0)，集M=ƒ(D)={ƒ(x)|x∈D}嶅Y称为函数ƒ的值域。函数ƒ:D→Y常常就看作ƒ:D→M。
在这个一般定义下，随着集D和M的不同，将得到不同类型的函数。
首先，如果M吇R，则称ƒ为实值函数。设ƒ是一个实值函数，如果还有D吇R，则ƒ显然就是以前谈到的一元（实）函数;如果D吇Rn（n维实欧氏空间），那么D的每个元素x为一个有序n实数组(x1，x2，…，xn)，这时人们常常用一个便于联想的名字来称呼函数──n 元(实)函数，并把函数y=ƒ(x)记作y=ƒ(x1，x2，…，xn)。如果n≥2，这样的 n元实函数统称为多元实函数。可以类似于一元实函数考虑多元实函数的图像。特别对二元实函数z=ƒ(x，y)(x，y∈D)来说，其图像，即集
{(x，y，z)｜(x，y∈D， z=ƒ(x，y)}常常可以在三维空间满意地作出，它为一张曲面。
如果D为实数集，M为复数集，这时称ƒ为实变元的复值函数；如果D和M都是复数集，这时称ƒ为含一个复变元的复值函数，常简称为单复变函数（见复变函数论）。
如果M吇Rm(m>1)，则称函数ƒ为向量值函数。向量值函数常以黑体字记之，如y =ƒ(x) ， g(x)等等。倘若还有D吇Rn，那么给定一个这样的向量值函数等价于给定m个n元实函数：
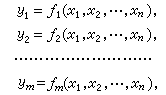
式中的函数ƒk(1≤k≤m)称为向量值函数ƒ 的第k个分量。向量值函数ƒ又常表示成
。
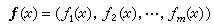定义域D为Rn的子集的向量值函数有时也叫做从集D到集M的变换或映射。
D吇R时，也就是定义域为实数集时的向量值函数专称它为纯量 x的向量值函数。一元实函数微积分学中的一些最基础的概念，如极限、导数、积分等等都比较容易地推广到这种向量值函数上。具体说来，设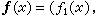
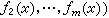是纯量x的向量值函数，那么可以通过以下的等式定义对ƒ 的极限、求导和积分运算：
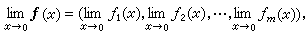
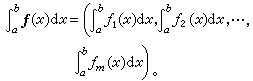
这里假定这些等式右端的有关分量都是有意义的。同样地，所谓这函数在某一区间上连续、可微、可积，也是指这函数的每个分量在所说的区间上具有相应的性质。在讨论几何与物理问题时，常常用到向量值函数。
推广了的函数的一般定义把诸如算子和泛函（包括某些广义函数）等概念都包含了进去，但是当D、M的元素是比数更抽象的数学对象时，人们还是愿意更多地使用那些专设的函数名称。