[拼音]:xiang he xiangbian
[外文]:phase and phase transition
一个处于热力学平衡状态的物质系统,可以是一个各处物理和化学性质都相同的均匀系;也可以由若干个有边界可分的均匀的部分组成,各部分之间的性质存在着差别;每一个均匀的部分叫做一个相。前类系统称为单相系;后类系统称为复相系。
物质的气态只有一种结构,多种气体互相混合,也只能形成一个均匀的单相。物质的液态一般只有一个相;液态氦则有两个相,分别称为氦Ⅰ和氦Ⅱ。两种不同的液体若能混合,则形成一个均匀相;若不能混合,如水和油,就会出现分界面,形成两相。物质的固态情况较复杂,结晶态可以有多种结构,它们分别属于不同的相。例如水在高压下有六种不同的结晶态,分别属于六种不同的相;又如硫的固态有单斜晶系和正交晶系两种结构,即两种相。而非晶态只有一个相。不同相之间发生的转变称为相变。如在低于临界压强下,气体的温度降到某一数值时就液化;在一定的压强下,把固体加热到某一温度时,发生熔解;铁磁性物质的温度上升到居里点以上时,其铁磁性就过渡到顺磁性;这些都是相变现象。
相变理论
相平衡曲线和克拉珀龙方程稳定在一定温度和压强下的物质的单相系,当温度和压强改变到某一范围内时,其稳定性遭到破坏,系统只有改变自己的结构才能得到新的稳定,这时出现两相或多相共存的稳定状态。对于单元系(只含一种化学组分的物质系统)两相共存的条件是:两相的温度T、压强p以及化学势μ都必须相等。根据
μ1(T,p)=μ2(T,p) (1)
这个条件,给出了两相共存时的压强对温度的依赖关系
p=p(T)。 (2)
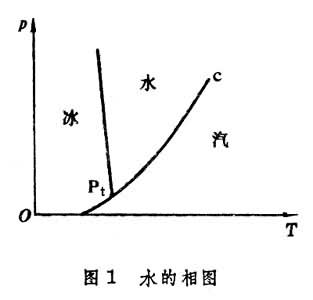
此式所描绘的曲线称为相平衡曲线。以p、T为直角坐标,描绘出相平衡曲线,曲线上的点表示两相共存状态,曲线两侧的区域是单相区,这个图形叫相图。
同一种物质的三相平衡应由式
μ1(T,p)=μ2(T,p)=μ3(T,p) (3)
确定,式中T、p代表三个相的共同温度和共同压强,三相共存的状态在相图上由孤立的点来表示,这个点称为三相点,它就是三条相平衡曲线的交点。热力学理论指出,对单元系来说,可以共存的相的数目不可能多于3(见吉布斯相律)。图1表示水的相图,Pt代表三相点。在适当的温度和压强范围,任何物质都有三相点。如果在相变过程中,伴随有一定热量的放出或吸收,则称这一热量为相变潜热。相图中的曲线都由实验测定,应用热力学理论则可求出曲线的斜率同潜热之间的关系为
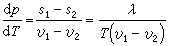 , (4)
, (4)
式中λ是1摩尔物质由2相变到1相的相变潜热,s1、s2、v1、v2分别是1相和2相的摩尔熵和摩尔体积。它描述了气-液相、液-固相和固-气相间的转变。此式是E.克拉珀龙于1834年得到的,由于R.克劳修斯应用热力学理论也导出了这个方程式,故又称克拉珀龙-克劳修斯方程,它表示当温度变化时,处于平衡的两相压强的变化。当温度和压强变到某个值,气液之间不再出现两相共存区,而是连续地过渡,则这点称为临界点(见图1中的c点)。例如水的临界点是Tc=374.15℃,pc=261.5标准大气压。临界点随不同的物质而异。可由下面方程决定
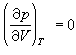 ,
,
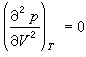 。 (5)
。 (5)
同时,临界态本身应当是稳定的,按热力学理论稳定性条件应是
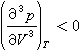 。 (6)
。 (6)
应当注意的是,满足稳定性条件的区域中,还有一部分属于亚稳状态,它们是过冷相或过热相。
 相变的级
相变的级
通常的相变发生在一定的压强和温度下,又称为一级相变。其特点是:两相的化学势相等,但化学势的一级偏导数所代表的性质发生突变,即摩尔熵和摩尔体积发生突变,但其改变为一有限量,有相变潜热。实验上还发现了另一类相变,称为二级相变。其特点是:两相的化学势和化学势的一级偏导数均相等;化学势的二级偏导数所代表的性质发生突变,且改变一有限量。也就是说,这类相变既无潜热,也无体积变化,但比热容、定压膨胀系数、等温压缩系数发生突变。三级相变的特点是:两相的化学势和化学势的一级、二级偏导数均相等,化学势的三级偏导数发生突变。M.von劳厄曾提出两种液态氦之间的相变属于第三级相变,可是未得到公认。倘若某种相变具有如下的特点:两相的化学势和化学势的一级、二级直至(n-1)级偏导数全相等,而n级偏导数发生突变,且改变量是有限的,这种相变称为n级相变。
厄任费斯脱二级相变方程P.厄任费斯脱在研究氦Ⅰ和氦Ⅱ之间的相变时,导出二级相变的厄任费斯脱方程
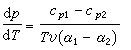 , (7)
, (7)
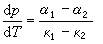 , (8)
, (8)
式中 сp、α、κ分别是定压比热容、定压膨胀系数和等温压缩系数。
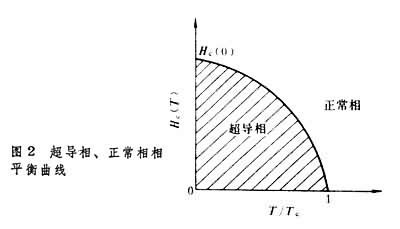
上述讨论可推广到其他物性,例如存在外磁场时超导态和正常态之间的相变情形。某些金属和合金在低于一定的转变温度(即临界温度)Tc时,电阻突然变为零,此时这些金属变为超导体,譬如铌的转变温度Tc为8.7K,锡为3.7K,在Tc之下,超导态也可以在一定的磁场值Hc下消失,转入正常态。实验给出Hc 和温度T(T<Tc)的曲线为
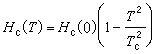 , (9)
, (9)
式中Hc(0)是当T→0K时Hc(T)的值。图2曲线两侧分别为超导相和正常相,故此曲线亦属相平衡曲线。按照热力学理论,超导相和正常相平衡时,它们的单位体积热力势g相等。
gs(T,Hc)=gn(T,Hc)。 (10)
从此式出发,即可得到以下形式的相平衡曲线方程式
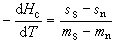 , (11)
, (11)
式中ss、ms分别是超导相的单位体积熵和磁化强度,sn、mn是对应正常相的量。其实只要把式(4)中的(p,υ)换成(-Hc,m)就行了。由于超导体又是一理想的抗磁体,故内部的磁感应强度等于零,则有
As=H+4πms=0。 (12)
而正常导体的磁导率μ一般约等于1,故mn=0,由式(11)和(12)即得
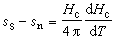 。 (13)
。 (13)
由图2看出,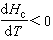 ,因此sn>ss。只有在T=Tc处,两相的单位体积熵相等。所以,可得出如下结论:
,因此sn>ss。只有在T=Tc处,两相的单位体积熵相等。所以,可得出如下结论:
(1)当T<Tc时,因外场存在而发生的相变有潜热,为一级相变;
(2)当T=Tc时的相变无潜热,属二级相变(忽略体积变化)。
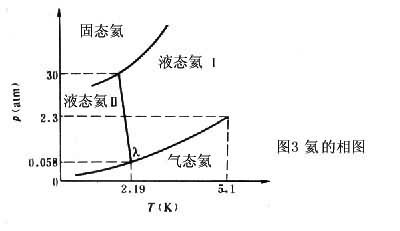
方程式(7)、(8)可用于cP、α、κ等量在突变点为有限的情形。除超导态和正常态在零磁场下的转变属于这类相变外,铁磁和顺磁相变,合金的有序和无序相变以及 HeⅠ-HeⅡ转变由于热容在相变点都是发散的,故都不适用,而把这类在突变点处热容呈现发散的二级相变称为λ相变。图3给出关于氦的实验相图,其中λ点是T=2.19K,p=0.058标准大气压。
 朗道二级相变理论
朗道二级相变理论
Л.Д.朗道从相变点处的对称性质的变化研究相变点领域的行为,他采用一个序参量 η来描述相变,η=0代表一种序比较低即对称性比较高的结晶状态,即无序态;η厵0则代表一种序比较高即对称性比较低的结晶状态, 即有序态。η是有序程度的量度,可由它所取的两种不同的值:或零,或有限值区分系统处于哪一相,而系统的热力学性质譬如热力势同 η有关。在一定的温度T和压强p之下,η的平衡值ηe同T、p有关,它由热力势的极小条件
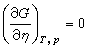 (14)
(14)
决定,由此式解出η=ηe(T,p),当T,p连续变到相变点时,ηe也连续地变为零。所有的相变点应是每个相的稳定性开始遭到破坏,或者稳定性条件
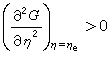 (15)
(15)
开始不适用的点,它处于稳定区和不稳定区的边界区域。对于二级相变来说,由于无共存区,因此,相变点是满足
ηe(T,p)=0 (16)
的临界态。由此式可画出相平衡曲线。
例如,铁磁体在居里温度以下,存在自发磁化,这属于在方向上对称性比较低的状态;当温度升高时,有序程度降低,自发磁化变小;当温度达到居里温度时,自发磁化等于零,此时系统处于对称性较高的状态,称为顺磁状态。于是可以把自发磁化作为序参量,它是一个矢量,记作ηi(i=1,2,3)。ηi=0代表顺磁态,ηi厵0代表铁磁态,ηi同T、p有关,其值由磁介质系统的热力势G(T,p,η)极小条件确定。关于超导相和正常相的相变问题,也可应用这种方法。朗道二级相变理论得出的结论是正确的,并且有相当的普遍性。
相变模型及其统计物理学解释
相变是极其普遍的现象,为了正确地阐明发生相变的机理,需要应用统计物理学理论。它对处于平衡态的系统给出了求配分函数的方法,但要具体求解,必须有相应的模型和手段。统计物理学关于相变问题的理论研究只能应用于一些简单的模型。
例如,非理想气体凝聚为液体时,物态方程要出现某种不连续性。图4表示在非理想气体的等温线上,对应于同一个pc,比容v=v(p)发生了一个突变。υ由气相比容υg变到液相比容υ1。
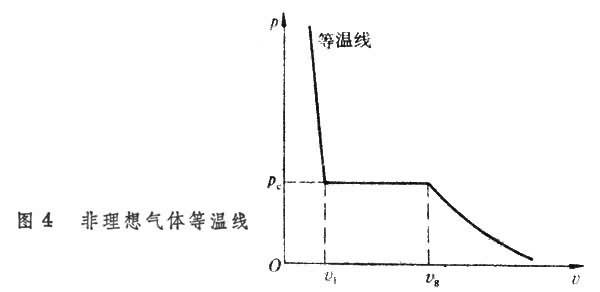
应用统计物理学理论可以得到如下结论:对于有限体积,系统没有异常行为,p-υ图上不可能发生凝聚现象,只有当体积V→∞时,才可得到由巨配分函数Ξ 所表示的热力学极限:
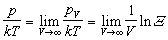 ,
,
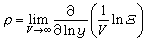 (17)
(17)
因而有可能发生如图4所示的相变,式中ρ为密度,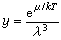 ,
,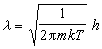 是热波长。李政道和杨振宁于1952年提出两条定理,论证了相变发生的可能性和条件。
是热波长。李政道和杨振宁于1952年提出两条定理,论证了相变发生的可能性和条件。
为了能在平衡态统计物理的范围内研究固体中的某些相变,人们提出了各种模型。
铁磁性模型当温度在居里温度以上时,铁(Fe)镍(Ni)这类金属中,原子自旋的取向是无规的,不产生净的磁矩;当温度低于居里温度时,原子的自旋自发地择优取向,结果在此方向发生自发磁化。当温度从高温一侧趋向居里温度时,比热容趋向无穷大,这是一种从非铁磁性状态到铁磁性状态的相变。铁磁性模型就是研究这类相变的一类简单的模型。
假设在周期性点阵的每个阵点上有一个自旋si(i=1,2,…),只考虑最近邻自旋之间的相互作用和每个自旋同外磁场的相互作用,则这个系统的哈密顿量应为
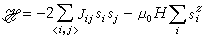 , (18)
, (18)
式中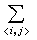 是对最近邻自旋对求和,H 是加在z方向上的外磁场强度,μ0是每个自旋的磁矩,
是对最近邻自旋对求和,H 是加在z方向上的外磁场强度,μ0是每个自旋的磁矩,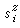 是第i个自旋算符的z方向分量,Jij是最近邻自旋对〈i,j〉的相互作用能或称交换积分,它仅同自旋间的距离有关,对于铁磁性物质Jij>0,对于反铁磁性物质Jij<0。具有这样的哈密顿量的铁磁性模型称为海森伯模型,若z方向分量对哈密顿量的贡献很小,可以略去,又x及y方向属各向异性,于是式(18)变为
是第i个自旋算符的z方向分量,Jij是最近邻自旋对〈i,j〉的相互作用能或称交换积分,它仅同自旋间的距离有关,对于铁磁性物质Jij>0,对于反铁磁性物质Jij<0。具有这样的哈密顿量的铁磁性模型称为海森伯模型,若z方向分量对哈密顿量的贡献很小,可以略去,又x及y方向属各向异性,于是式(18)变为
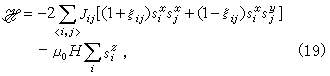
式中ξij是决定于自旋i和j之间距离的常数,这个模型称为XY 模型。若磁各向异性是z方向分量对哈密顿量的贡献占绝对优势,而x、y方向分量的贡献可以忽略时,则式(18)变为
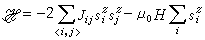 , (20)
, (20)
式中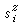 取值+1/2或-1/2。这时,不考虑式(18)的哈密顿量所具有的算符对易性这个量子力学效应。这种模型就是在相变理论中占有重要地位的伊辛模型。略去上标z,并取s=±1,
取值+1/2或-1/2。这时,不考虑式(18)的哈密顿量所具有的算符对易性这个量子力学效应。这种模型就是在相变理论中占有重要地位的伊辛模型。略去上标z,并取s=±1,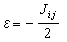 ,就得到伊辛模型哈密顿量常用的表示
,就得到伊辛模型哈密顿量常用的表示
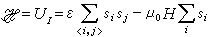 , (21)
, (21)
式中ε为最近邻自旋对相互作用能量。对于铁磁物质ε<0;反铁磁物质ε>0。
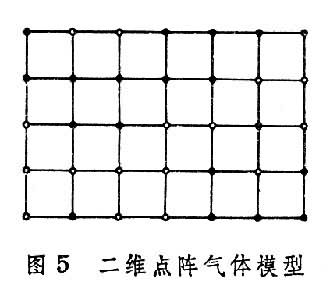
点阵气体模型是一种非真实气体模型,按照这个模型,N 个可分辨的粒子排列在周期点阵的N0个阵点上,每个阵点最多只能为一个粒子占据,每个粒子仅同其最近邻的粒子发生作用。
图5是二维点阵气体模型的示意图,图中“。”代表空位,“·”代表阵点上有粒子占据。这种模型是为了便于将伊辛模型所研究的铁磁性相变同一般的气-液相变进行比较并作统一考虑而提出的。这N个粒子系统的总能量为
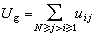 , (22)
, (22)
式(22)中uij是i、j阵点上的两个粒子的相互作用能,如以rij表示粒子i和粒子j的距离,则
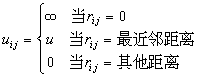 (23)
(23)
 有序-无序相变
有序-无序相变
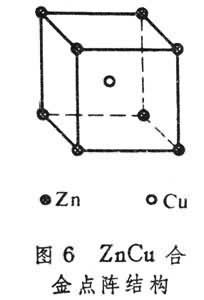
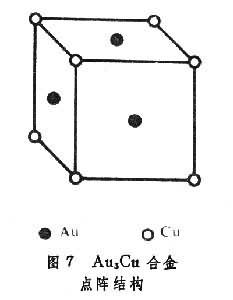
这是一个实际问题。如体心立方结构的锌铜合金(ZnCu合金),面心立方结构的金三铜合金(Au3Cu合金),它们的点阵分别由两套简单立方格子和四套简单立方格子构成,如图6和图7所示。实验证明:当温度T→Tc(相变温度)时,比热容c→∞。当T<Tc时,合金中不同原子的占位是有序的;当T升高时,这种占位的有序化逐渐被破坏;当T>Tc时,就完全被破坏。每个阵点对于各种原子来说都是等价的,因而占位是无规的。这种相变称为有序-无序相变。认为处于阵点上的粒子仅同其最近邻阵点上的粒子之间存在着相互作用。以 N 和N
和N 和N
和N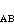 分别代表最近邻为 AA、BB和 AB的最近邻对总数,NA、NB和N0分别表示A原子总数、B原子总数和总阵点数,ε
分别代表最近邻为 AA、BB和 AB的最近邻对总数,NA、NB和N0分别表示A原子总数、B原子总数和总阵点数,ε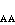 、ε
、ε 和ε
和ε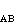 分别表示最近邻对AA、BB和AB的相互作用能。则有序-无序相变系统的相互作用总能量为
分别表示最近邻对AA、BB和AB的相互作用能。则有序-无序相变系统的相互作用总能量为
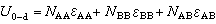 。 (24)
。 (24)
伊辛模型、点阵气体模型和有序-无序相变问题中的UI、Ug和U0-d经过简单的运算以后可以写成相似的形式,所以在计算它们的配分函数或诸热力学量时也可用统一的方法处理。对伊辛模型的计算结果,也可以用到其他两个问题上。
方法
20世纪30、40年代以来,许多科学家对上述的几种相变模型求解,采用的方法主要有平均场近似、高温展开和低温展开、解析法、数值法以及重正化群方法等。
平均场近似它是处理伊辛模型的一种近似方法。对于三维的真实情形,须作某种近似,即P.外斯的平均场理论。考虑把每个阵点的自旋si都用由下式
 (25)
(25)
定义的一个序参量 η 来代替。显然,当 时,全部自旋的磁矩都同磁场平行,磁极化达到了饱和,此时η=1;当
时,全部自旋的磁矩都同磁场平行,磁极化达到了饱和,此时η=1;当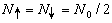 时,整个系统磁化为零,η=0。可见η是描述系统极化状态的参量。用独立的自旋在等效的外磁场H┡中的势能代替各对自旋的相互作用能。任何一个自旋(不管向上或向下)所受到的最近邻自旋的作用均等于H┡,在一定的温度下
时,整个系统磁化为零,η=0。可见η是描述系统极化状态的参量。用独立的自旋在等效的外磁场H┡中的势能代替各对自旋的相互作用能。任何一个自旋(不管向上或向下)所受到的最近邻自旋的作用均等于H┡,在一定的温度下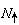 和
和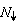 的平均值是一定的,因此,
的平均值是一定的,因此,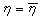 具有一定的值。可以得到自洽方程
具有一定的值。可以得到自洽方程
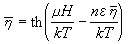 。 (26)
。 (26)
不存在外磁场(H=0)时上式变为
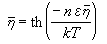 。 (27)
。 (27)
用图解法求出在ε<0(铁磁性物质)情形下的解
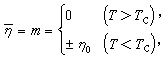 (28)
(28)
式中Tc是居里温度
 , (29)
, (29)
η0是式(27)的大于零的根。在T=0和T=Tc附近,得到近似值
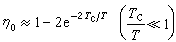 ,
,
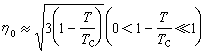 , (30)
, (30)
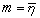 是磁化强度。还可以求出能量、熵、亥姆霍兹自由能(见自由能)等各个热力学量,当T>Tc时,它们都等于零,当T<Tc时,它们都是η0的偶函数。这表明存在由式(29)给出的临界温度Tc,在Tc以上,当H=0时,物质不磁化;在Tc以下,尽管H=0,但磁化强度不为零,它可正可负,且无论磁化强度是正还是负,热力学函数均相同,故在临界温度以下,铁磁性物质存在相变。
是磁化强度。还可以求出能量、熵、亥姆霍兹自由能(见自由能)等各个热力学量,当T>Tc时,它们都等于零,当T<Tc时,它们都是η0的偶函数。这表明存在由式(29)给出的临界温度Tc,在Tc以上,当H=0时,物质不磁化;在Tc以下,尽管H=0,但磁化强度不为零,它可正可负,且无论磁化强度是正还是负,热力学函数均相同,故在临界温度以下,铁磁性物质存在相变。
20世纪40年代L.昂萨格对一维、二维伊辛模型采用解析法,获得了不存在外磁场条件下的严格解,表明:一维伊辛模型不存在相变,二维的在一定条件下发生相变。这种方法具有指导性的意义。
临界指数和标度假定是凝聚和相变问题的一个重要方面,它作为研究物质的相变现象和临界性质的一种有效手段,近20年来有了很大的发展。
由实验知道,各种物质发生相变时,随着温度趋近临界温度Tc,物理量一般以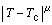 的规律变化,μ是描述相转变的指数,称为临界指数。
的规律变化,μ是描述相转变的指数,称为临界指数。
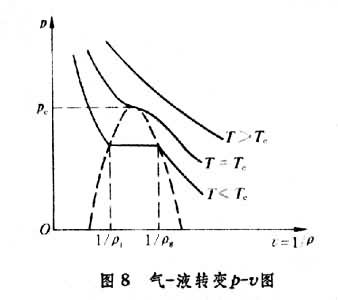
图8中虚线表示气、液两相共存曲线,在它之下为二相区。当T<Tc(临界温度)时,液体密度ρ1同气体密度ρg差别很大,但达到Tc时,ρ1同ρg的差别趋于消失。这个特征表示存在一个序参量,它在Tc以上取值为零,在Tc以下,取非零的值,在这里可取序参量为ρ1-ρg,于是有
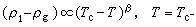 , (31)
, (31)
式中β>0称为临界指数,由实验确定。实验指出,等温压缩系数κT和定容比热容cV,当T=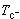 或
或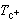 时,均发散。其实由图8看出
时,均发散。其实由图8看出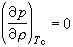 ,因而κT→∞,仿照式(31),也可定义κT和cV的临界指数,它们分别为-γ,-γ┡和-α,-α┡。
,因而κT→∞,仿照式(31),也可定义κT和cV的临界指数,它们分别为-γ,-γ┡和-α,-α┡。
对于磁性系统,序参量取为自发磁化强度,并用下述一般公式定义临界指数b,即可写成
 , (32)
, (32)
根据式(32)列表1。表中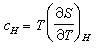 ,
,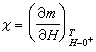 ,m为磁化强度,r为分子间距离,d 为系统维数。表1共列出9个临界指数:-α、-α┡、β、-γ、-γ┡、δ、-v、-v┡、η。发现铁磁性和液体两个系统的临界指数-α、β、-γ、δ 均非常接近。将伊辛模型分别用平均场近似、二维昂萨格严格解和计算机数字解计算六个临界指数得到的数值和各种铁磁物质相应的临界指数的实验值列于下表。
,m为磁化强度,r为分子间距离,d 为系统维数。表1共列出9个临界指数:-α、-α┡、β、-γ、-γ┡、δ、-v、-v┡、η。发现铁磁性和液体两个系统的临界指数-α、β、-γ、δ 均非常接近。将伊辛模型分别用平均场近似、二维昂萨格严格解和计算机数字解计算六个临界指数得到的数值和各种铁磁物质相应的临界指数的实验值列于下表。

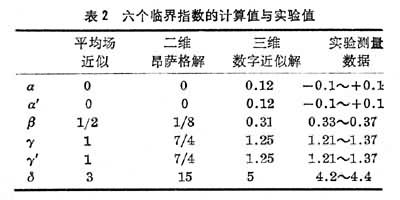
可见利用各种模型和方法算出的临界指数虽互不相同,但它们之间的某些关系对于各种模型和方法来说几乎完全相同,并同实验的测量结果符合。从此表容易看出,α、α┡、β、γ、γ┡和δ之间满足以下关系
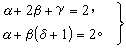 (33)
(33)
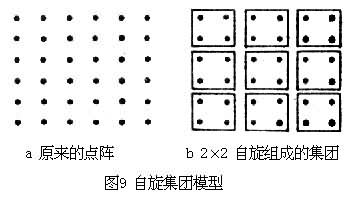
此式是联系各临界指数的关系式,称为标度律。1966年前后,L.P.卡达诺夫从标度假设出发,推出这些关系式。考虑伊辛模型,引入参量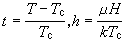 ,现讨论由每边L个自旋组成的集团,L=2情形如图9所示,假设标度变换为
,现讨论由每边L个自旋组成的集团,L=2情形如图9所示,假设标度变换为
tL=tLa,hL=hLb, (34)
并认为在临界温度附近,以参量t、h的自旋元胞问题同tL、hL的自旋集团问题等价,即有每个自旋的热力势的关系式
g(tL,hL)=Lbg(t,h)。 (35)
注意式(34)中指数a、b不能由标度假设确定。那么运用式(35)及一些热力学关系式,容易推导出各临界指数同a、b的关系式,从而得到如下标度律
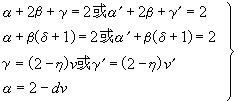 。 (36)
。 (36)
这样,标度假设就把9个临界指数并为两个独立指数,因此这个假设是可取的,所得到的标度律非常有用,但对这个假设的解释尚不清楚。
 重正化群法
重正化群法
1971年K.G.威耳孙推广量子场论中重正化群方法,把它用于相变和临界现象中,得到了很好的结果,他也因此获得1982年诺贝尔物理学奖。
相变理论处理的问题是一个十分复杂的多体问题,必须采用减少自由度的办法来解决。标度变换体现了重正化群变换的基本思想,不去直接计算配分函数,而是讨论那些使配分函数保持不变的变换性质,从而抓住相变的主要特征。
重正化群变换性质有两个步骤:
(1)进行粗粒平均,由于当T=Tc时,关联长度ξ→∞,则元胞自旋可用集团平均值代替、相互作用可用自旋集团间的有效作用代替。若每个集团内有n个自旋,则在坐标空间的平均为
 。 (37)
。 (37)
也可在动量空间平均,完成对自旋变量的傅氏变换,
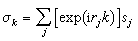 (38)
(38)
短波部分的积分。这样,“尺子变长”,分辨率降低,关联长度(见相关函数)也相应地缩小了。
(2)进行标度变换,使其同原来模型一致。对尺度: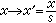 ,
,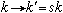 ,整个系统收缩s倍;对自旋
,整个系统收缩s倍;对自旋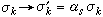 ,这好像用倍数低的显微镜观察,当然就不能看到细节的情况。把①、②两步合起来的变换用Rs表示,得到哈密顿量的变换式
,这好像用倍数低的显微镜观察,当然就不能看到细节的情况。把①、②两步合起来的变换用Rs表示,得到哈密顿量的变换式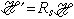 ,Rs一般是非线性变换。可以证明
,Rs一般是非线性变换。可以证明
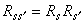 。 (39)
。 (39)
故这个变换形成半群,称为重正化群。经过以上手续把同其自由度有关系的相互作用重新作了调整,因而减少了自由度。再把Rs变换下的不动点同连续相变联系起来分析连续相变下的特征。