[拼音]：liang
[外文]：beam
承受垂直于轴线的横向载荷的杆件。它是工程结构中重要的承力构件，如房梁、轮船的龙骨、飞机机翼的大梁和起重机的大梁。梁的种类繁多，按照轴线形状，可分为直梁和曲梁；按照支持的形式，可分为悬臂梁、简支梁、连续梁、弹性基础梁等（图1）。梁的支反力可由静力平衡条件确定的，称为静定梁，（见静定结构），如悬臂梁和简支梁；不能由静力平衡条件确定的，称为静不定梁（见静不定结构），如连续梁和弹性基础梁。
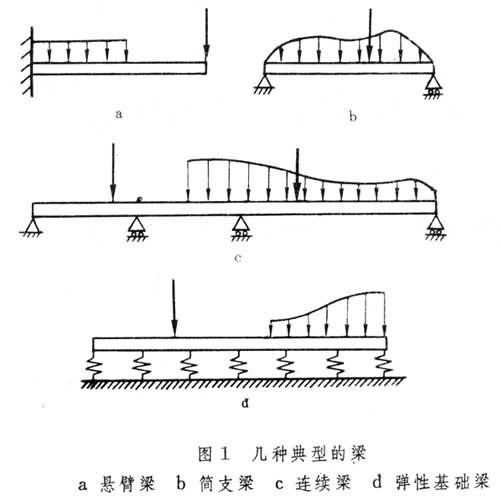
在横向载荷作用下，梁轴线的曲率会发生变化，直梁的轴线由直变曲，曲梁轴线的曲率增大或减小。这类变形称为弯曲变形，变形后的轴线称为挠曲线。
早在17世纪，伽利略就研究过梁的弯曲问题。在随后的一百多年中，经E.马略特、雅各布第一.伯努利(见伯努利家族)、A.帕伦、C.-A.de库仑等科学家的继续研究，基本上形成以平截面假设为基础的弯曲理论。这一近似理论满足了工程上的要求并得到广泛的应用。
弯曲形式若梁的横截面有一对称轴，则梁有一纵向对称面。梁的轴线即为纵向对称面内的直线（直梁情形）或曲线（曲梁情形）。若作用于梁上的载荷都在这个纵向对称面内，则挠曲线也是这一平面内的曲线，这类弯曲称为平面弯曲，是工程中最常见的弯曲形式。若梁的横截面无对称轴，则梁也无纵向对称面，但只要载荷通过弯心连线，且平行于截面的形心主惯性轴（见截面的几何性质），梁的变形仍为平面弯曲。在横截面无对称轴的情况下，如果载荷通过弯心但不平行于截面的形心主惯性轴，则梁在两个形心主惯性平面内同时产生弯曲变形，变形后的挠曲线不再位于载荷作用的纵向平面内，这种弯曲称为非对称弯曲。若梁的横截面虽有对称轴，而载荷通过截面形心而不与对称轴重合，梁也会在两个形心主惯性平面内同时弯曲，变形后的挠曲线也不在载荷作用的纵向平面内，这种弯曲有时称为斜弯曲。
剪力图和弯矩图对横向载荷作用下的梁（图2a），
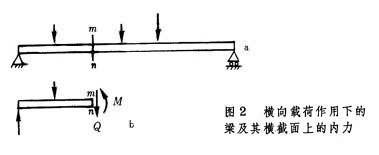
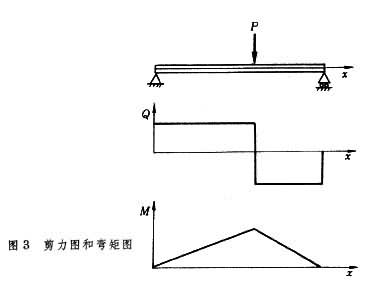
用假想的横截面mn把梁截开。由于每一部分处于平衡状态，所以在截面mn上，必然有一个分布的内力系，它代表mn截面左右两部分之间的相互作用。根据平衡条件，截面上的内力系可用一个大小为Μ的力矩和一个与截面相切的、大小为Q的力代替(图2b)，前者称为mn截面上的弯矩，后者称为mn截面上的剪力。不同截面上的弯矩和剪力一般不相同。在实际问题中，为便于计算梁内的应力和梁的变形，常用图表示剪力和弯矩随截面位置的变化，这些图称为剪力图和弯矩图。例如图3中在集中力P作用下的简支梁，其剪力和弯矩分别如其下的两折线所示。图中横坐标x表示截面位置，纵坐标分别为该截面上的剪力Q和弯矩Μ。若在梁的某一部分内，截面上只有弯矩而无剪力，则这一部分梁的弯曲称为纯弯曲；既有弯矩又有剪力的弯曲，称为横力弯曲。
弯曲正应力
每一梁截面上的弯矩都由截面上的弯曲正应力所平衡。由梁截面上的弯矩可进一步求出截面上正应力的分布规律。根据平截面假设，梁内必然存在一个变形前后纤维长度不改变的中性层。它把梁分为两部分，一部分受拉，另一部分受压。中性层和横截面的交线称为中性轴（图4）。
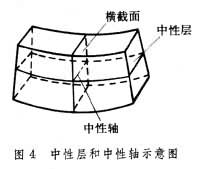
对直梁来说，弯曲变形后挠曲线上一点的曲率半径ρ和该点所在截面上的弯矩Μ之间有以下关系：
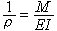， (1)
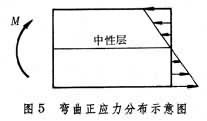
式中E为材料的弹性模量；I为截面对中性轴的惯性矩。EI反映了梁抵抗弯曲变形的能力，称为弯曲刚度。梁内任一纤维的受力和变形，与它到中性层的距离成正比，即横截面上任意点的弯曲正应力与该点到中性轴的距离成正比，如图5所示。图中正应力用右侧的箭头表示。弯曲正应力的计算公式为：
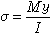， (2)
式中σ为横截面上一点的正应力值；y为该点到中性轴的距离。由于横截面上离中性轴越远的点的正应力越大，所以，为了充分利用材料，应尽可能把材料置放于离中性轴较远处。这样梁能以较小的弯曲变形抵抗弯矩的作用。采用工字梁或箱形梁的道理就在于此。
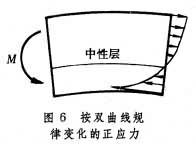
上述直梁弯曲理论，在纯弯曲的情况下是精确的。如果把它应用于横力弯曲，所得结果是近似的，但对比较细长的梁其精确度已可满足工和要求。对轴线曲率半径远大于横截面高度的曲梁，仍然可以使用式(2)。但如果轴线曲率半径和横截面高度的量级相同(如吊钩)，则正应力沿截面高度的变化规律为双曲线(图6)，而不再象直梁那样按直线规律分布。
弯曲剪应力
在横力弯曲下，梁截面上除了有与弯矩对应的正应力外，还有与剪力对应的弯曲剪应力。剪应力的分布与梁的几何形状有关，它在变截面梁和等截面梁中的分布也有很大差异。用材料力学的方法，可以计算截面呈某些特殊形状的杆件的剪应力。例如，在狭长矩形截面梁中，剪应力沿截面的高度按抛物线规律分布（图7）。图中左边的箭头表示剪应力的方向，右边的阴影表示剪力的大小。在中性轴上，剪应力最大(τ嚝)，而在横截面上下边缘，剪应力等于零。
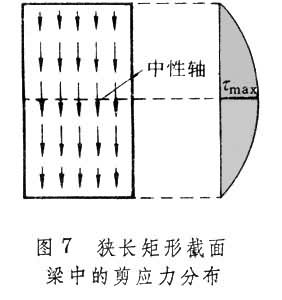
在梁的弯曲问题中，弯曲正应力是主要的，弯曲剪应力是次要的，有时可忽略。但对于一些特殊情况的梁，如跨度较短的梁、薄腹板梁、夹层梁等，剪应力不可忽略。
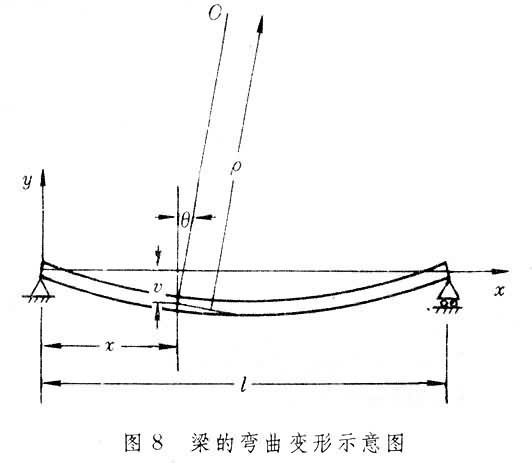
弯曲变形在如图8所示的坐标系中，以v表示直梁平面弯曲挠曲线上一点的纵坐标，则挠曲线的方程式可以写作：
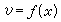， (3)
v就是横坐标为x的梁截面形心的垂直位移，称为挠度。梁截面在弯曲变形中对其原来的位置所转过的角度θ 称为该截面的转角。工程中常见的直梁，其挠曲线是一非常平坦的曲线，即挠度v远小于跨度l，转角θ也非常小。这样，截面转角θ近似地等于挠曲线上对应点的斜率tgθ，即
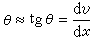。 (4)
而曲率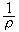
也可近似地写成：
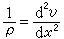。 (5)
将上式中的曲率代入公式(1)，得出挠曲线的近似微分方程式：
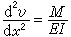。 (6)
根据以上方程式，通过积分法、共轭梁法或差分法等，就可求得截面转角及挠度。
以上的讨论，都假设材料是线弹性的，服从胡克定律。若应力超出弹性范围，材料中就会出现塑性变形。在这种情况下，平截面假设仍然有效，但应力－应变关系不再是线性的，且在加载和卸载过程中遵循不同的规律。在考虑塑性变形的基础上研究梁的弹塑性弯曲问题，会得出一些不同的结果（见塑性力学）。