[拼音]：tuoyuanxing pianweifen fangcheng
[外文]：partial differential equation of elliptic type
简称椭圆型方程，一类重要的偏微分方程。早在1900年D.希尔伯特提的著名的23个问题中，就有三个问题(第19、20、23问题)是关于椭圆型方程与变分法的。八十多年来，椭圆型方程的研究获得了丰硕的成果。椭圆型方程在流体力学、弹性力学、电磁学、几何学和变分法中都有应用。拉普拉斯方程是椭圆型方程最典型的特例。
拉普拉斯方程许多定常的物理过程，如稳定的热传导过程、牛顿引力理论及电磁理论中的位势、弹性薄膜的平衡、不可压流体的定常运动等，提出形如
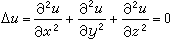(1)
的方程，称之为拉普拉斯方程，以及泊松方程
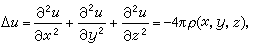(2)
式中ρ一般有密度的意义。
容易得到方程(1)和(2)的一些特解。由于方程是线性的，因此可以由已知的一些特解叠加而得到新的解。积分也是一种叠加。通过积分型叠加，便可得到方程(1)的如下的重要解：
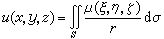(3)
式中S为一曲面，μ为定义在S上的连续函数。由(3)确定的函数u在S以外的地方满足方程(1)。
非齐次方程(2)有一个重要的特解，它就是以ρ为密度的体位势：
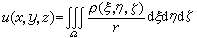(4)
只要ρ在域Ω内有界且连续可微，由(4)确定的函数u在Ω内就满足方程(2)，而在Ω外则满足方程(1)。
在应用上，往往不是求一些特解，而是求满足某些附加条件的解。例如，第一边值问题（狄利克雷问题）：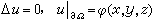
；第二边值问题（诺伊曼问题）：
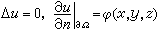。这里Ω为(x，y，z)空间的一个有界域，φ为定义在边界嬠Ω上的已知连续函数，n为嬠Ω的单位外法向量。
这些边值问题的解的惟一性，由调和函数的一个极值性质很容易推出。拉普拉斯方程的二次连续可微解，称为调和函数。
极值原理域Ω内的调和函数不可能在域内一点取极大值或极小值，除非这个调和函数恒等于常数。若调和函数的最大值只在某一边界点 p上达到，则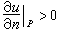
（假设u在p点可微）。
这些边值问题的解的存在性，也不难证明。由格林公式可以推得
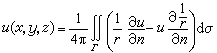(5)
从而有
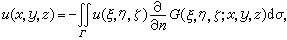
式中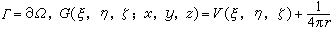
，
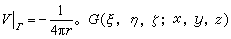称为拉普拉斯方程关于域Ω的格林函数。由此引出解第一边值问题的如下方法：先求出G(ξ，η，ξ；x，y，z)，再将所给的边界值代入，得到
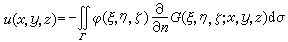(6)只要对边界面再加上一些限制，就可以证明由(6)确定的函数u是第一边值问题的解。应当指出，对于某些特殊域，如球、半球、半空间等，格林函数是容易用镜像法求得的。以球域为例，设K是以原点为中心、R为半径的球体，关于球体K的格林函数就是
，
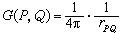
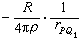式中Q1是向径OQ的延长线上的一个点，它使
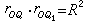（如图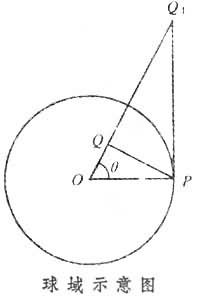
所示）。点Q1为点Q关于球面S=嬠K的反演点。将G(p，Q)代入(6)即得到泊松公式：
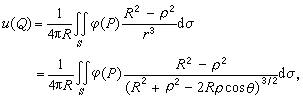
它所确定的函数 u(Q)就是拉普拉斯方程关于球域K的第一边值问题的解。
利用泊松公式和极值原理，可以推出调和函数的一系列基本性质，如平均值公式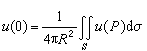
、调和函数的解析性、哈那克定理等等。
公式(5)中出现的积分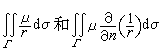
，分别称为展布在曲面Г上密度为μ的单层位势和双层位势。它们都是Ω内的调和函数。单层位势通过边界面是连续的，而双层位势在边界面上有跳跃。因此为了使双层位势满足第一边值问题的边界条件，必须选取μ使它满足积分方程
，
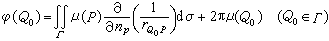由于这一积分方程是齐次的，除平凡解外无其他连续解，因此，按弗雷德霍姆定理，该方程对任何φ恒可解。这样，以这个解为密度的双层位势便给出了第一边值问题的解。利用单层位势和弗雷德霍姆定理，同样可以证明第二边值问题的可解性。上述积分方程法虽然能统一地处理第一边值问题和第二边值问题，但是对域的边界要求过严，如要求它是鲁古诺夫曲面。
关于第一边值问题的解的存在性论证有许多更一般，的方法，如庞加莱-佩隆方法、施瓦兹交替法、差分法等。
第一边值问题，还可用变分法求解。古典的变分法理论指出，如果函数u=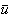
(x，y，z)适合第一边值问题的边界条件，且使泛函（狄利克雷积分）
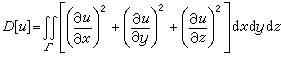(7)
取极值，则当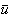
∈C2(Ω)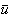，必满足这一泛函的欧拉-拉格朗日方程，即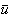是拉普拉斯方程(1)的解。这种把一泛函的极值问题归结为解微分方程的边值问题，是变分法早期的理论。但是这一理论只有在极少的特殊情形才是可行的。因此人们产生了与此相反的思考，用求解泛函极值问题来获得微分方程边值问题的解。（G.F.）B.黎曼由泛函(7)的非负性作出断：(7)必存在极小值函数，它就是狄利克雷问题的解。这个论断称为狄利克雷原理。K.（T.W.）外尔斯特拉斯指出了黎曼在提出这个论断时逻辑上的不严密，并举出了有下界而无极小值的泛函的例子。多年之后，首先由希尔伯特给出了狄利克雷原理的完整无缺的证明。其他的证明也随之相继出现，这方面的研究极大地推动了泛函分析的发展，也使得变分法成为研究偏微分方程的强有力的工具。
形如
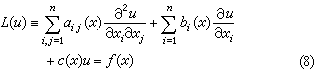
的方程，若(αij(x))为正定的矩阵，则称为椭圆型的；若(αij(x)) 的最大特征值与最小特征值之比有界，则方程(8)称为一致椭圆型的。经常考虑的是方程(8)的如下三种边值问题;①第一边值问题（狄利克雷问题），其边界条件为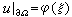
。
（2）第二边值问题(诺伊曼问题)，其边界条件为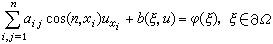
。
（3）第三边值问题(混合问题)，其边界条件为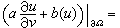
φ(ξ)，这里α可在嬠Ω的部分点集上为0，v方向与补法线方向夹角小于π/2。
二阶椭圆型方程的研究甚早，在50年代以前，对方程(8) 的一些基本边值问题的可解性就获得某些成果。在几十年的发展中，建立了各种解法，例如，绍德尔方法、泛函方法、差分法、变分法、积分方程法，等等。
绍德尔方法是建立在绍德尔估计之上的。设 Ck+α表示k次连续可微且k阶微商α 赫德尔连续的函数类，又设Ω是Rn中的C2+α区域，方程(8)的所有系数和自由项都属于Cα。所谓绍德尔估计，是指若方程(8)在Ω中有解u，并且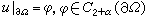
，则
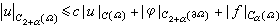
式中с是一个与方程(8)和区域有关的常数。
在上述假设下，由泊松方程具有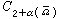
解u以及一般线性方程的极值原理，当с≤0时可以得
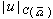的估计。因此利用绍德尔估计和参数的连续开拓就可以证明方程(8) 的狄利克雷问题的解的存在性。作为极值原理的一个直接推论：当с≤0时狄利克雷问题的解是惟一的。
泛函方法肇端于K.O.弗里德里希斯1934年关于对称椭圆算子半有界扩张的工作。H.外尔，C.Л.索伯列夫、C.Γ.米赫林和М.И.维希克等人在40年代末期的进一步研究表明，解椭圆型方程的基本边值问题等价于解形如x＋AX＝ƒ的算子方程，其中A是希尔伯特空间的全连续算子。从而由泛函分析的里斯－绍德尔理论得到椭圆型方程可解性的所谓“二择一原理”。
近几十年来椭圆型方程的重大进展之一，是解拟线性椭圆型方程
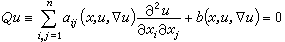(9)
通常用勒雷－绍德尔不动点原理。
设B是巴拿赫空间，T是从B×[0，1]到B的一个完全连续映射，对所有x∈B，使得T(x，0)=0。若存在M，使得对满足x＝T(x，t)的所有(x，t)∈B×[0，1]，有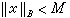
，则T1x＝T(x，1)在B中有不动点。这就是勒雷-绍德尔不动点原理。
考虑问题簇
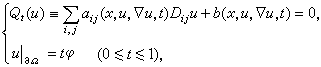
式中Q1＝α，Qt对所有t∈[0，1]都是椭圆的。定义u＝T(υ，t)是线性狄利克雷问题
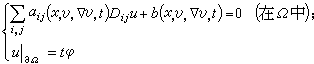
的惟一解。于是可以看出，方程(9)的狄利克雷问题的解u就是T(υ，1)的不动点。通常取B为C1+β，0<β<1。对系数加以适当限制就可使得T满足勒雷－绍德尔原理的要求，于是方程(9)的狄利克雷问题就化为求问题簇的C1+β(捙)解的先验估计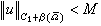
。
形如下面的方程组
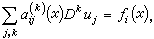(10)
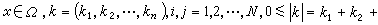
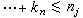，此处，对一切x∈Ω，一切ξ∈Rn-[0]，
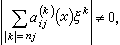是最一般线性椭圆型方程组。这个定义是И.Γ.彼得罗夫斯基给出的。
对于如此广泛的方程组，有些人例如，L.赫尔曼德尔讨论过它的一般边值问题：
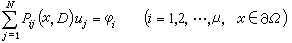
此处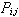
(x，D)是变系数的微分算子，nj与μ之间存在着某种关系。
这样的边值问题，一般经典的弗雷德霍姆备择定理不成立。维希克和L.尼伦伯格等人提出了一个子类，称之为强椭圆组，对于它的某些基本边值问题，弗雷德霍姆备择定理是成立的。
近年来，研究在流形上定义的椭圆算子的一大成就是阿蒂亚－辛格指标定理。