[拼音]：yashengsu liudong
[外文]：subsonic flow
流体在流场中所有各点处的流速，都低于当地声速（见声速）的流动。亚声速气流流过静止物体时，在雷诺数较高的情况下，粘性的影响常只局限于物面附近的边界层和物体下游的尾流区内，因此，在分析许多流动问题时，粘性可以忽略，即把全部流动视为无粘性流动。一般所说的亚声速流动常常是指这种无粘流体的亚声速流动。
对这种无粘亚声速流动作理论研究的原因有两方面：首先，实际气体运动的基本方程太复杂，很难求解，而对一些具体问题，例如计算机翼的举力，粘性的影响很小，可以忽略，使基本方程简化，便于求解。其次，对于某些流动问题（例如机翼的阻力），即使粘性不能忽略，也可以在无粘流的理论基础上再考虑粘性影响，进行求解。
流动特点亚声速流动和超声速流动的主要区别有两方面：
（1）流速v与流管横截面积A的关系不同。在定常流动中，沿流管存在下列关系：
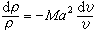， (1)
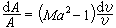， (2)
式中v为流速;Μa为当地马赫数；ρ为气体密度。在亚声速流动中(Μa<1)，密度相对变化│dρ/ρ│小于速度的相对变化。在低马赫数时，例如在Μa≤0.3的范围内，可以完全忽略密度的变化;把气体视为不可压缩流体（即ρ为常数），这种低马赫数下的亚声速流动称为低速流动或不可压缩流动。对于不可压缩流动，ρ为常量，研究起来容易得多。ρ为变量的流动称为可压缩流动，其中Μa恒小于1的流动即为亚声速流动，Μa恒大于1的流动称为超声速流动。由上式可以看出，不管是亚声速流动还是超声速流动，如速度增加，密度就减小。但就流管横截面积A而言，在亚声速时，若A减小，则流速增大；在超声速时，若A增大，则流速也增大（见气体动力学）。
（2）当物体在静止气体中运动时，如果运动速度低于声速，则它对气体的扰动可传播到全流场；当运动速度超过声速时，扰动的范围是有限的。若把物体看成是一个点扰源，扰动局限于扰源的后马赫锥内（见超声速流动），而传不到物体的远前方。
基本方程式流体流动时服从自然界的一些普遍规律，如质量守恒，动量守恒，能量守恒等。表达这些规律的方程式，称为基本方程式。无粘匀直流流过静止物体时，若流动是亚声速的，从理论上可以证明，流动一定是无旋的，有速度势ф(x，y，z)存在，在直角坐标系中它与速度的关系为：
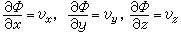， (3)
式中vx、vy、vz分别为沿 x、y、z方向的分速。由于存在速度势ф，可以将运动学和动力学分开，只须求出一个未知函数ф，问题大为简化。下面给出用速度势ф表示的低亚声速流动和亚声速流动的基本方程式：
（1）低亚声速流动（不可压缩流动） 此时Μa≤0.3，可以忽略密度变化，将流动视为不可压缩流动。基本方程为下列拉普拉斯方程：
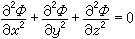。 (4)
方程(4)是线性的，可以先找出一些基本解，然后应用解的叠加原理求出满足具体边界条件的解。对于定常流动（见非定常流动），例如无粘匀直流绕过静止物体的流动，在速度势ф求出后，由式(3)即可求出流场中的速度分布vx、vy、vz。再利用不可压缩流动的伯努利方程(见伯努利定理)，就可求出流场中的压强分布p(x，y，z)和物面上的压强分布，于是可以很容易地求出物体所受的作用力（例如机翼的举力）。
分析无粘不可压缩流动问题的关键在于根据具体的边界条件，求拉普拉斯方程(4)的解。 对于复杂的物形（边界条件也复杂），例如整架飞机，要用计算机求解。如果物形比较简单，例如大展弦比直机翼（这是低速飞机常用的一种机翼），可用一些近似理论（如举力线理论、举力面理论）近似求解。对平面不可压缩位势流问题，除速度势ф(x，y)外，还存在流函数Ψ(x，y)，两者的关系为：
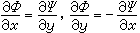， (5)
式(5)在数学上称为柯西-黎曼条件，在此条件下存在复位势：
w(x+iy)=ф(x，y)+iΨ(x，y)， (6)
式中i=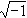
。这样，解具体流动的问题，就化为按具体边界条件求复位势ω 的问题。利用复变函数理论中的保角变换法，可以较容易地求解条件较复杂的流动问题。
（2）亚声速流动 无粘匀直流流过静止物体时是等熵流动，而且存在速度势ф(x，y，z)，它服从下述基本方程：
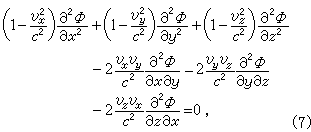
式中c为当地声速。方程(7)为非线性方程，很难求解，对于低亚声速流动（即不可压缩流动），c→∞，上式就变成拉普拉斯方程(4)。从物理意义上说，亚声速流动与不可压缩流动在流动特点上没有本质上的不同，就方程而言，式(4)和式(7)都属于椭圆型偏微分方程，所以亚声速流动与不可压缩流动只有量的差别。由于不可压缩流动的理论和实验研究都已取得一定的结果，可根据不可压缩流动这些结果，作一些量的修正，得出相应的亚声速流动的结果。在小扰动条件下的修正方法有普朗特－格劳厄脱法则，卡门－钱学森公式等。
方程(7)中所有各项的系数都只是速度的函数(声速c也可以通过能量方程化为速度的函数)，因而对于平面流动在以速度分量vx、vy为直角坐标的速度面上，该方程变成线性的，可以应用叠加原理求问题的解。这种方法称为速度图法。在速度图法中，基本方程是线性化的、简单的。但对具体问题，边界条件却复杂化了，求精确解仍存在很大困难。